题目内容
如图,已知∠EFD=∠BCA,BC=EF,AF=DC.则AB=DE.请说明理由.(填空)
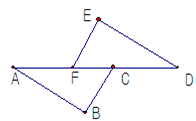
解:∵AF=DC(已知)
∴AF+ =DC+
即
在△ABC和△DEF中
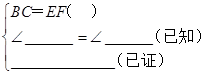
∴△ABC≌△DEF( )
∴则AB=DE

解:∵AF=DC(已知)
∴AF+ =DC+
即
在△ABC和△DEF中
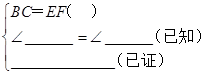
∴△ABC≌△DEF( )
∴则AB=DE
FC,FC,AC=DF,已知,EFD,BCA,AC=DF,SAS
试题分析:由AF=DC可得AC=DF,再结合∠EFD=∠BCA,BC=EF可证得△ABC≌△DEF,问题得证.
∵AF=DC(已知)
∴AF+FC=DC+FC
即AC=DF
在△ABC和△DEF中

∴△ABC≌△DEF( SAS )
∴则AB=DE.
点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
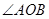 的平分线方法如下:以
的平分线方法如下:以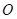 为圆心,任意长为半径画弧交
为圆心,任意长为半径画弧交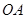 、
、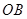 于
于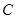 、
、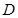 ,再分别以点
,再分别以点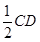 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点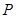 ,作射线
,作射线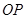 ,由作法得
,由作法得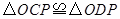 的根据是( )
的根据是( )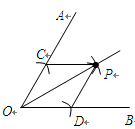
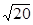 ;
;
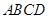 ,
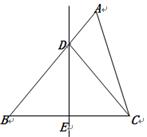
,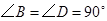 ,把纸片按如图所示折叠,使点
,把纸片按如图所示折叠,使点 落在
落在 边上的
边上的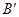 点,
点, 是折痕.
是折痕.
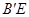 与
与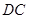 的位置关系;
的位置关系;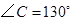 ,求
,求 的度数.
的度数.