题目内容
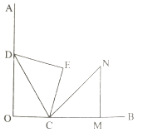
【题目】如图![]() ,
,![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 上,则
上,则![]() 值为()
值为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由等腰直角三角形的性质∠EDC=∠ECD=45°,从而CE=![]() CD,由旋转的性质得:∠MCN=∠DCE=∠ECD=45°,CM=CE=
CD,由旋转的性质得:∠MCN=∠DCE=∠ECD=45°,CM=CE=![]() CD,∠DCN=75°,求出∠DCM=120°,得出∠OCD=60°,由锐角三角函数的知识求出OD=
CD,∠DCN=75°,求出∠DCM=120°,得出∠OCD=60°,由锐角三角函数的知识求出OD=![]() CD,即可得出答案.
CD,即可得出答案.
∵等腰三角形△CDE的顶点D、C在OA、OB上,∠M=90°,
∴∠EDC=∠ECD=45°,CE=![]() CD,
CD,
由旋转的性质得:∠MCN=∠DCE=∠ECD=45°,CM=CE=![]() CD,∠DCN=75°,
CD,∠DCN=75°,
∴∠DCM=45°+75°=120°,
∴∠OCD=60°,
∴OD=sin60°×CD=![]() CD,
CD,
∴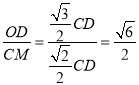 ;
;
故选B.

练习册系列答案
相关题目
【题目】某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 | 乙 | 丙 | |
平均数 | 7.9 | 7.9 | 8.0 |
方差 | 3.29 | 0.49 | 1.8 |
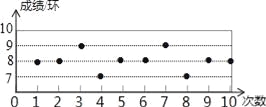
根据以上图表信息,参赛选手应选( )
A. 甲 B. 乙 C. 丙 D. 丁