题目内容
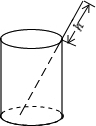 如图,将一根长9cm的筷子,置于底面直径为3cm,高为4cm的圆柱形水杯中,设筷子露在杯子外面的长度是为hcm,则h的取值范围是
如图,将一根长9cm的筷子,置于底面直径为3cm,高为4cm的圆柱形水杯中,设筷子露在杯子外面的长度是为hcm,则h的取值范围是4<h<5
4<h<5
.分析:根据杯子内筷子的长度取值范围得出杯子外面长度的取值范围,即可得出答案.
解答:解:∵将一根长9cm的筷子,置于底面直径为3cm,高为4cm的圆柱形水杯中,
∴在杯子中筷子最短是等于杯子的高,最长是等于杯子斜边长度,
∴当杯子中筷子最短时等于杯子的高,h=9-4=5(cm),
当杯子中筷子最长时等于杯子斜边长度,h=9-
=4(cm),
∴h的取值范围是:4<h<5.
故答案为:4<h<5.
∴在杯子中筷子最短是等于杯子的高,最长是等于杯子斜边长度,
∴当杯子中筷子最短时等于杯子的高,h=9-4=5(cm),
当杯子中筷子最长时等于杯子斜边长度,h=9-
| 32+42 |
∴h的取值范围是:4<h<5.
故答案为:4<h<5.
点评:此题主要考查了勾股定理的应用,正确得出杯子内筷子的取值范围是解决问题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
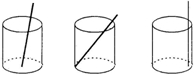 如图所示,将一根长24cm的筷子,置于底面直径为9cm,高为12cm的圆柱形水杯中,如图,设筷子露出在杯子外面的部分长为hcm,则h的取值范围是
如图所示,将一根长24cm的筷子,置于底面直径为9cm,高为12cm的圆柱形水杯中,如图,设筷子露出在杯子外面的部分长为hcm,则h的取值范围是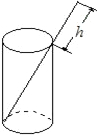 如图,将一根长24cm的筷子放入底面直径为5cm,高为12cm的圆柱形水中,设筷子露在被子外面的长度为hcm,则h的最小值是( )
如图,将一根长24cm的筷子放入底面直径为5cm,高为12cm的圆柱形水中,设筷子露在被子外面的长度为hcm,则h的最小值是( )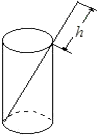 如图,将一根长24cm的筷子放入底面直径为5cm,高为12cm的圆柱形水中,设筷子露在被子外面的长度为hcm,则h的最小值是
如图,将一根长24cm的筷子放入底面直径为5cm,高为12cm的圆柱形水中,设筷子露在被子外面的长度为hcm,则h的最小值是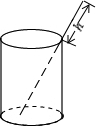 如图,将一根长9cm的筷子,置于底面直径为3cm,高为4cm的圆柱形水杯中,设筷子露在杯子外面的长度是为hcm,则h的取值范围是________.
如图,将一根长9cm的筷子,置于底面直径为3cm,高为4cm的圆柱形水杯中,设筷子露在杯子外面的长度是为hcm,则h的取值范围是________.