题目内容
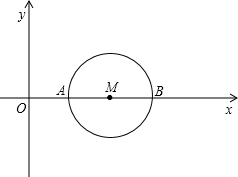
如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B,已知抛物线y=| 1 |
| 6 |
(1)求点C的坐标,并画出抛物线的大致图象;
(2)求出抛物线的顶点D的坐标,并确定与圆M的位置关系;
(3)点Q(8,m)在抛物线y=
| 1 |
| 6 |
分析:(1)根据⊙M圆心的坐标和半径的长,可表示出A、B两点的坐标,代入抛物线的解析式中,即可求得待定系数的值,从而确定该抛物线的解析式,也就能得到点C的坐标.
(2)将抛物线的解析式化为顶点坐标式,即可求得点D的坐标;由于抛物线和圆都是轴对称图形,那么点D、M都在抛物线的对称轴上,可根据圆的半径来判定点D和圆M的位置关系.
(3)根据抛物线的解析式,即可确定点Q的坐标;由于A、B关于抛物线对称轴对称,那么连接QA,直线QA与抛物线对称轴的交点即为所求的点P,此时PQ+PB的最小值为QA的长,根据Q、A的坐标即可求得QA的长,由此得解.
(2)将抛物线的解析式化为顶点坐标式,即可求得点D的坐标;由于抛物线和圆都是轴对称图形,那么点D、M都在抛物线的对称轴上,可根据圆的半径来判定点D和圆M的位置关系.
(3)根据抛物线的解析式,即可确定点Q的坐标;由于A、B关于抛物线对称轴对称,那么连接QA,直线QA与抛物线对称轴的交点即为所求的点P,此时PQ+PB的最小值为QA的长,根据Q、A的坐标即可求得QA的长,由此得解.
解答: 解:(1)由已知,得A(2,0),B(6,0),
解:(1)由已知,得A(2,0),B(6,0),
∵抛物线y=
x2+bx+c过点A和B,则:
,
解得
;
则抛物线的解析式为y=
x2-
x+2.
故C(0,2).(3分)
(说明:抛物线的大致图象要过点A、B、C,其开口方向、顶点和对称轴相对准确)(4分)
 (2)由(1)得:y=
(2)由(1)得:y=
x2-
x+2=
(x-4)2-
;
故D(4,-
),D点在圆内.(7分)
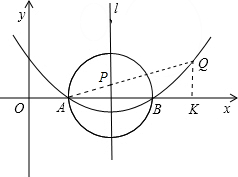
(3)如图,抛物线对称轴l是x=4;
∵Q(8,m)抛物线上,
∴m=2;
过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6,
∴AQ=
=2
;(10分)
又∵B(6,0)与A(2,0)关于对称轴l对称,
∴PQ+PB的最小值=AQ=2
.(12分)
 解:(1)由已知,得A(2,0),B(6,0),
解:(1)由已知,得A(2,0),B(6,0),∵抛物线y=
| 1 |
| 6 |
|
解得
|
则抛物线的解析式为y=
| 1 |
| 6 |
| 4 |
| 3 |
故C(0,2).(3分)
(说明:抛物线的大致图象要过点A、B、C,其开口方向、顶点和对称轴相对准确)(4分)
 (2)由(1)得:y=
(2)由(1)得:y=| 1 |
| 6 |
| 4 |
| 3 |
| 1 |
| 6 |
| 2 |
| 3 |
故D(4,-
| 2 |
| 3 |
(3)如图,抛物线对称轴l是x=4;
∵Q(8,m)抛物线上,
∴m=2;
过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6,
∴AQ=
| AK2+QK2 |
| 10 |
又∵B(6,0)与A(2,0)关于对称轴l对称,
∴PQ+PB的最小值=AQ=2
| 10 |
点评:此题主要考查了二次函数解析式的确定、顶点坐标的求法以及平面展开-最短路径等相关知识,难度适中.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是