题目内容
 (2012•甘孜州)如图,两个半圆外切,它们的圆心都在x轴的正半轴上,并都与直线y=x相切.若半圆O1的半径为1,则半圆O2的半径R=
(2012•甘孜州)如图,两个半圆外切,它们的圆心都在x轴的正半轴上,并都与直线y=x相切.若半圆O1的半径为1,则半圆O2的半径R=3+2
| 2 |
3+2
.| 2 |
分析:作O1A⊥直线y=x于A,作O2B⊥直线y=x于B,O1C⊥O2B于C,则O1C∥直线y=x,所以∠CO1O2=∠AOO1,由于直线y=x平分∠xoy,即∠AOO1=45°,得到∠CO1O2=45°,判断△CO1O2为等腰直角三角形,然后根据切线的性质和两圆相切的性质得O1A=1,O2B=R,O1O2=R+1,再根据等腰直角三角形的性质得到O1O2=
O2C,即R+1=
(R-1),最后解关于R的方程即可.
| 2 |
| 2 |
解答: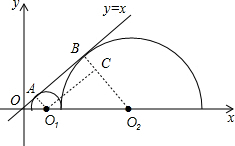 解:作O1A⊥直线y=x于A,作O2B⊥直线y=x于B,O1C⊥O2B于C,如图,
解:作O1A⊥直线y=x于A,作O2B⊥直线y=x于B,O1C⊥O2B于C,如图,
则O1C∥直线y=x,
∴∠CO1O2=∠AOO1,
∵直线y=x平分∠xoy,
∴∠AOO1=45°,
∴∠CO1O2=45°,
∴△CO1O2为等腰直角三角形,
∵⊙O1和⊙O2与直线y=x相切,
∴O1A=1,O2B=R,
∴BC=1,O2C=R-1,
而⊙O1和⊙O2外切,
∴O1O2=R+1,
∴O1O2=
O2C,即R+1=
(R-1),
∴R=3+2
.
故答案为3+2
.
 解:作O1A⊥直线y=x于A,作O2B⊥直线y=x于B,O1C⊥O2B于C,如图,
解:作O1A⊥直线y=x于A,作O2B⊥直线y=x于B,O1C⊥O2B于C,如图,则O1C∥直线y=x,
∴∠CO1O2=∠AOO1,
∵直线y=x平分∠xoy,
∴∠AOO1=45°,
∴∠CO1O2=45°,
∴△CO1O2为等腰直角三角形,
∵⊙O1和⊙O2与直线y=x相切,
∴O1A=1,O2B=R,
∴BC=1,O2C=R-1,
而⊙O1和⊙O2外切,
∴O1O2=R+1,
∴O1O2=
| 2 |
| 2 |
∴R=3+2
| 2 |
故答案为3+2
| 2 |
点评:本题考查了圆的综合题:熟练掌握切线的性质和两圆相切的性质以及第一象限的角平分线的解析式;会运用等腰直角三角形的性质进行计算.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 (2012•甘孜州)如图放置的圆锥,它的主视图、俯视图、左视图分别为( )
(2012•甘孜州)如图放置的圆锥,它的主视图、俯视图、左视图分别为( )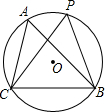 (2012•甘孜州)如图.⊙O是△ABC的外接圆,∠CAB=65°,P是⊙O上的一点,则∠CPB等于( )
(2012•甘孜州)如图.⊙O是△ABC的外接圆,∠CAB=65°,P是⊙O上的一点,则∠CPB等于( ) (2012•甘孜州)如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )
(2012•甘孜州)如图是某班学生最喜欢的球类活动人数统计图,则下列说法不正确的是( )