Question

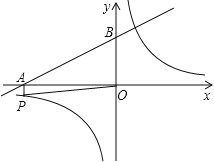
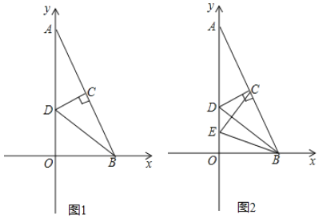
【题目】如图1，在平面直角坐标系中，，，的垂直平分线交轴与点，连接，为第一象限内的点．

（1）求点坐标；

（2）当时，求的值；

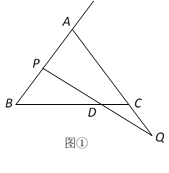
（3）如图2，点为轴上的一个动点，当为等腰三角形时，直接写出点的坐标．

Answer 1

【答案】（1）;(2)a=6;(3) 或 或 或

【解析】

（1）设OD=x，则AD=8-x，由线段垂直平分线的性质得BD=AD=8-x，在Rt△BOD中，由勾股定理得出方程，解方程即可得出D点坐标；

（2）设直线BD的解析式为y=kx+b，由待定系数法即可得出解析式，由题意得出△DBC与△DBM是同底等高的三角形，得出BD与直线CM平行，求出直线CM的解析式为 ；把M(a，1)代入，求出a=6即可；

（3）由勾股定理求出AB，得出 ，由勾股定理求出 ，分三种情况：①EC=ED时，②DC=DE时；③CE=CD时；分别求出点E的坐标即可.

解：（1）∵B(4，0)，A(0，8)

∴OA=8，OB=4

设OD=x，则AD=8-x

∵AB的垂直平分线交与y轴于点D

∴BD=AD=8-x

在Rt△BOD中，由勾股定理得：

∴x=3

∴D(0，3)

(2)设直线BD的解析式为y=kx+b，

把B(4，0)和D(0，3)代入y=kx+b得：

∴

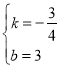
则直线BD的解析式为

∵ 时，

∴△DBC与△DBM同是底为BD，且高相等的三角形

∴直线BD与直线CM平行

设CM的解析式为 ，

∵CD是AB的垂直平分线

∴C是AB的中点

∵B(4，0)，A(0，8)，

∴C(2，4)

把C(2，4)代入得：，

解得：

∴直线CM的解析式为

又因为M(a，1)且在第一象限

∴

解得：a=6

（3）由勾股定理得，

∵点C为边AB的中点

∴

∵AD=OA-OD=5

∴

设E(0，x)，则

分三种情况：①EC=ED时， 过E作EQ⊥CD于Q，如图所示：

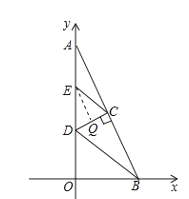
则EQ∥AB

∴Q为CD的中点

∴E为AD的中点

∴AE=ED

∴8-x=x-3

解得：

②DC=DE时

∴

∴ 或

∴ 或

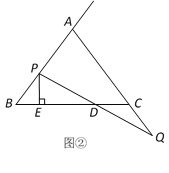
③CE=CD时，过C作CF⊥AO交于F，如图所示：

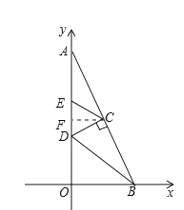
∴∠AFC=∠AOB=90°F为ED中点

∴FC//OB，EF=DF

∵C为AB的中点

∴F为AO的中点，

∵A(0，8)，O(0，0)

∴F(0，4)

∴EF=DF=1

∴x-4=1

∴x=5

∴E(0，5)

综上所述：当△CDE为等腰三角形时，E点的坐标为或 或 或