ĢāÄæÄŚČŻ
”¾ĢāÄæ”æ×ŪŗĻÓėĢ½¾æ
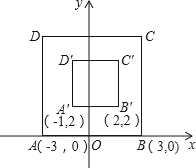
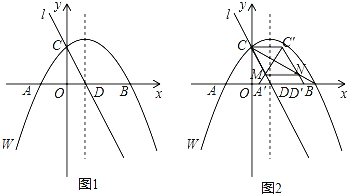
ČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Å×ĪļĻßWµÄŗÆŹż±ķ“ļŹ½ĪŖy=©![]() x2+
x2+![]() x+4£®Å×ĪļĻßWÓėxÖį½»ÓŚA£¬BĮ½µć£ØµćBŌŚµćAµÄÓŅ²ą£¬ÓėyÖį½»ÓŚµćC£¬ĖüµÄ¶Ō³ĘÖįÓėxÖį½»ÓŚµćD£¬Ö±Ļßl¾¹żC”¢DĮ½µć£®
x+4£®Å×ĪļĻßWÓėxÖį½»ÓŚA£¬BĮ½µć£ØµćBŌŚµćAµÄÓŅ²ą£¬ÓėyÖį½»ÓŚµćC£¬ĖüµÄ¶Ō³ĘÖįÓėxÖį½»ÓŚµćD£¬Ö±Ļßl¾¹żC”¢DĮ½µć£®
(1)ĒóA”¢BĮ½µćµÄ×ų±ź¼°Ö±ĻßlµÄŗÆŹż±ķ“ļŹ½£®
(2)½«Å×ĪļĻßWŃŲxÖįĻņÓŅĘ½ŅʵƵ½Å×ĪļĻßW”䣬ÉčÅ×ĪļĻßW”äµÄ¶Ō³ĘÖįÓėÖ±Ļßl½»ÓŚµćF£¬µ±”÷ACFĪŖÖ±½ĒČż½ĒŠĪŹ±£¬ĒóµćFµÄ×ų±ź£¬²¢Ö±½ÓŠ“³ö“ĖŹ±Å×ĪļĻßW”äµÄŗÆŹż±ķ“ļŹ½£®
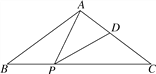
(3)ČēĶ¼2£¬Į¬½ÓAC£¬CB£¬½«”÷ACDŃŲxÖįĻņÓŅĘ½ŅĘmøöµ„Ī»£Ø0£¼m”Ü5£©£¬µĆµ½”÷A”äC”äD”䣮ÉčA”äC½»Ö±ĻßlÓŚµćM£¬C”äD”ä½»CBÓŚµćN£¬Į¬½ÓCC”䣬MN£®ĒóĖıߊĪCMNC”äµÄĆ껿£ØÓĆŗ¬mµÄ“śŹżŹ½±ķŹ¾£©£®
”¾“š°ø”æ£Ø1£©µćA×ų±źĪŖ£Ø©3£¬0£©£¬µćBµÄ×ų±źĪŖ£Ø7£¬0£©£¬y=©2x+4£»(2) µćFµÄ×ų±źĪŖ£Ø5£¬©6£©£¬y=©![]() x2+
x2+![]() x£»(3) ĖıߊĪCMNC”äµÄĆ껿ĪŖ
x£»(3) ĖıߊĪCMNC”äµÄĆ껿ĪŖ![]() m2.
m2.
”¾½āĪö”æ
øł¾ŻÅ×ĪļĻߵĽāĪöŹ½£¬Įīy£½0¼“æÉĒó³öĮ½µćµÄ×ų±ź.øł¾ŻÅ×ĪļĻߵĽāĪöŹ½æÉ·Ö±šĒó³öC£¬DĮ½µćµÄ×ų±ź£¬ŌŁÓĆ“ż¶ØĻµŹż·Ø¼“æÉĒó³öÖ±Ļߵıķ“ļŹ½.
øł¾ŻĢāŅā£¬ĄūÓĆ½ĒµÄµČĮæ¹ŲĻµæÉŅŌµĆµ½”Ļ1£½”Ļ3£¬½ų¶ųµĆµ½tan”Ļ1£½tan”Ļ3£¬øł¾ŻČż½ĒŗÆŹżµÄ¼ĘĖć·½·ØĮŠ³öµČŹ½£¬øł¾ŻŅ»“ĪŗÆŹżµÄ½āĪöŹ½Éčµć![]() µÄ×ų±źĪŖ£ØxF£¬©2xF£«4£©£¬½«ø÷Ļ߶ĪµÄ³¤¶Č“śČėµČŹ½¼“æÉĒó³öµćFµÄ×ų±ź£¬ŌŁøł¾ŻĘ½ŅʵķØŌņ¼“æÉĒó³öw”äµÄ±ķ“ļŹ½.
µÄ×ų±źĪŖ£ØxF£¬©2xF£«4£©£¬½«ø÷Ļ߶ĪµÄ³¤¶Č“śČėµČŹ½¼“æÉĒó³öµćFµÄ×ų±ź£¬ŌŁøł¾ŻĘ½ŅʵķØŌņ¼“æÉĒó³öw”äµÄ±ķ“ļŹ½.
øł¾ŻĘ½ŅĘ£¬æÉŅŌµĆµ½µćC”䣬A”䣬D”äµÄ×ų±ź£¬ŌŁøł¾Ż“ż¶ØĻµŹż·ØæÉŅŌµĆµ½Ö±ĻßA”äC”䣬BC£¬C”äD”äµÄ½āĪöŹ½£¬øł¾Ż½»µćµÄ¼ĘĖć·½·ØĮŠ·½³Ģ×éæÉŅŌĒóµĆµćM£¬NµÄ×ų±ź£¬øł¾ŻĘ½ŅʵĶØŅåŗĶĘ½ŠŠĖıߊĪµÄ¶ØŅåæÉÖŖĖıߊĪCMNC”äŹĒĘ½ŠŠĖıߊĪ£¬ŌŁøł¾ŻĘ½ŠŠĖıߊĪĆ껿µÄ¼ĘĖć·½·ØæÉŅŌµĆµ½Ę½ŠŠĖıߊĪCMNC”äµÄĆ껿.
£Ø1£©µ±y£½0Ź±£¬©![]() x2£«
x2£«![]() £«4£½0£¬½āµĆx1£½©3£¬x2£½7£¬
£«4£½0£¬½āµĆx1£½©3£¬x2£½7£¬
”ąµćA×ų±źĪŖ£Ø©3£¬0£©£¬µćBµÄ×ų±źĪŖ£Ø7£¬0£©£®
”ß©![]() £½
£½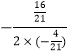
”ąÅ×ĪļĻßwµÄ¶Ō³ĘÖįĪŖÖ±Ļßx£½2£¬
”ąµćD×ų±źĪŖ£Ø2£¬0£©£®
µ±x£½0Ź±£¬y£½4£¬
”ąµćCµÄ×ų±źĪŖ£Ø0£¬4£©£®
ÉčÖ±ĻßlµÄ±ķ“ļŹ½ĪŖy£½kx£«b£¬
![]()
½āµĆ![]()
”ąÖ±ĻßlµÄ½āĪöŹ½ĪŖy£½©2x£«4£»
(2)”ßÅ×ĪļĻßwĻņÓŅĘ½ŅĘ£¬Ö»ÓŠŅ»ÖÖĒéæö·ūŗĻŅŖĒó£¬
¼“”ĻFAC£½90”ć£¬ČēĶ¼.
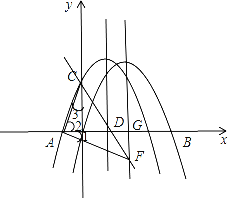
“ĖŹ±Å×ĪļĻßw”äµÄ¶Ō³ĘÖįÓėxÖįµÄ½»µćĪŖG£¬
”ß”Ļ1£«”Ļ2£½90”ć”Ļ2£«”Ļ3£½90”ć£¬
”ą”Ļ1£½”Ļ3£¬
”ątan”Ļ1£½tan”Ļ3£¬
”ą![]() =
=![]() £®ÉčµćFµÄ×ų±źĪŖ£ØxF£¬©2xF£«4£©£¬
£®ÉčµćFµÄ×ų±źĪŖ£ØxF£¬©2xF£«4£©£¬
”ą![]() £½
£½![]() £¬½āµĆxF£½5£¬©2xF£«4£½©6£¬
£¬½āµĆxF£½5£¬©2xF£«4£½©6£¬
”ąµćFµÄ×ų±źĪŖ£Ø5£¬©6£©£¬“ĖŹ±Å×ĪļĻßw”äµÄŗÆŹż±ķ“ļŹ½ĪŖy£½©![]() x2£«
x2£«![]() x£»
x£»
(3)ÓÉĘ½ŅĘæÉµĆ£ŗµćC”䣬µćA”䣬µćD”äµÄ×ų±ź·Ö±šĪŖC”ä£Øm£¬4£©£¬A”ä£Ø©3£«m£¬0£©£¬D”ä£Ø2£«m£¬0£©£¬CC”ä”ĪxÖį£¬C”äD”ä”ĪCD£¬
æÉÓĆ“ż¶ØĻµŹż·ØĒóµĆ
Ö±ĻßA”äC”äµÄ±ķ“ļŹ½ĪŖy£½![]() x£«4©
x£«4©![]() m£¬
m£¬
Ö±ĻßBCµÄ±ķ“ļŹ½ĪŖy£½©![]() x£«4£¬
x£«4£¬
Ö±ĻßC”äD”äµÄ±ķ“ļŹ½ĪŖy£½©2x£«2m£«4£¬
·Ö±š½ā·½³Ģ×é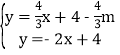 ŗĶ
ŗĶ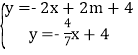
½āµĆ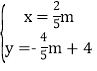 ŗĶ
ŗĶ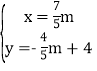
”ąµćMµÄ×ų±źĪŖ£Ø![]() m£¬©
m£¬©![]() m£«4£©£¬µćNµÄ×ų±źĪŖ£Ø
m£«4£©£¬µćNµÄ×ų±źĪŖ£Ø![]() m£¬©
m£¬©![]() m£«4£©£¬
m£«4£©£¬
”ąyM£½yN
”ąMN”ĪxÖį£¬
”ßCC”ä”ĪxÖį£¬
”ąCC”ä”ĪMN£®
”ßC”äD”ä”ĪCD£¬
”ąĖıߊĪCMNC”äŹĒĘ½ŠŠĖıߊĪ£¬
”ąS£½m[4©£Ø©![]() m£«4£©]
m£«4£©]
£½![]() m2
m2

 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
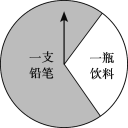
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø”¾ĢāÄæ”æijÉĢ³”ÓŠŅ»øöæÉŅŌ×ŌÓÉ×Ŗ¶ÆµÄŌ²ŠĪ×ŖÅĢ£ØČēĶ¼£©£®¹ę¶Ø£ŗ¹ĖæĶ¹ŗĪļ100ŌŖŅŌÉĻæÉŅŌ»ńµĆŅ»“Ī×Ŗ¶Æ×ŖÅĢµÄ»ś»į£¬µ±×ŖÅĢĶ£Ö¹Ź±£¬ÖøÕėĀäŌŚÄÄŅ»øöĒųÓņ¾Ķ»ńµĆĻąÓ¦µÄ½±Ę·£ØÖøÕėÖøĻņĮ½øöÉČŠĪµÄ½»Ļߏ±£¬µ±×÷ÖøĻņÓŅ±ßµÄÉČŠĪ£©£®ĻĀ±ķŹĒ»ī¶Æ½ųŠŠÖŠµÄŅ»×éĶ³¼ĘŹż¾Ż£ŗ
×Ŗ¶Æ×ŖÅĢµÄ“ĪŹżn | 100 | 150 | 200 | 500 | 800 | 1000 |
ĀäŌŚ”°Ē¦±Ź”±µÄ“ĪŹżm | 68 | 111 | 136 | 345 | 546 | 701 |
ĀäŌŚ”°Ē¦±Ź”±µÄʵĀŹ £Ø½į¹ū±£ĮōŠ”ŹżµćŗóĮ½Ī»£© | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
£Ø1£©×Ŗ¶ÆøĆ×ŖÅĢŅ»“Ī£¬»ńµĆĒ¦±ŹµÄøÅĀŹŌ¼ĪŖ_______£»£Ø½į¹ū±£ĮōŠ”ŹżµćŗóŅ»Ī»£©
£Ø2£©Ē¦±ŹĆæÖ»0.5ŌŖ£¬ŅūĮĻĆæĘæ3ŌŖ£¬¾Ķ³¼ĘøĆÉĢ³”ĆæĢģŌ¼ÓŠ4000Ćū¹ĖæĶ²Ī¼Ó³é½±»ī¶Æ£¬Ēė¼ĘĖćøĆÉĢ³”ĆæĢģŠčŅŖÖ§³öµÄ½±Ę··ŃÓĆ£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬øĆÉĢ³”Ļė°ŃĆæĢģÖ§³öµÄ½±Ę··ŃÓĆæŲÖĘŌŚ3000ŌŖ×óÓŅ£¬Ōņ×ŖÅĢÉĻ”°Ņ»ĘæŅūĮĻ”±ĒųÓņµÄŌ²ŠÄ½ĒÓ¦µ÷ÕūĪŖ______¶Č£®
”¾ĢāÄæ”æŌŚ¶ž“ĪŗÆŹży£½£x2£«bx£«cÖŠ£¬ŗÆŹżyÓė×Ō±äĮæxµÄ²æ·Ö¶ŌÓ¦ÖµČēĻĀ±ķ£ŗ
x | ”” | £2 | 0 | 3 | 4 | ”” |
y | ”” | £7 | m | n | £7 | ”” |
Ōņm”¢nµÄ“󊔹ŲĻµĪŖ( )
A. m£¾n B. m£¼n C. m£½n D. ĪŽ·ØČ·¶Ø