题目内容
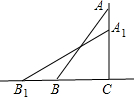 如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑2米,那么它的底端滑动多少米?
如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑2米,那么它的底端滑动多少米?
分析:已知AB,AC,在直角△ABC中即可计算BC,梯子下滑2米,即CA1=6米,A1B1=AB=10米,在直角△CA1B1中,根据勾股定理即可计算CB1,底端滑动的距离为CB1-CB.
解答:解:由题意知AB=10米,AC=8米,在直角△ABC中,BC=
=6米,
当顶端下滑2米,即即CA1=6米,则在直角△CA1B1中,A1B1=AB=10米,
∴CB1=
=8米,
底端滑动距离为CB1-CB=8米-6米=2米.
答:梯子底端滑动2米.
| AB2-AC2 |
当顶端下滑2米,即即CA1=6米,则在直角△CA1B1中,A1B1=AB=10米,
∴CB1=
| ( B1A1)2-CA12 |
底端滑动距离为CB1-CB=8米-6米=2米.
答:梯子底端滑动2米.
点评:本题考查了勾股定理在实际生活中的应用,本题中根据梯子长不会变的等量关系求解是解题的关键.

练习册系列答案
相关题目
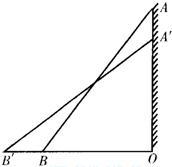 15、如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯
15、如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯
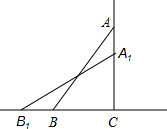 如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑1米,那么它的底端滑动多少米?如果梯子的顶端沿墙下滑2米,那么梯足将向外移多少米?
如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑1米,那么它的底端滑动多少米?如果梯子的顶端沿墙下滑2米,那么梯足将向外移多少米?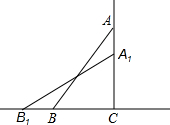 如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑1米,那么它的底端滑动多少米.
如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑1米,那么它的底端滑动多少米.