题目内容
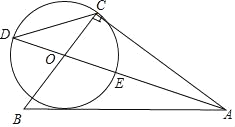
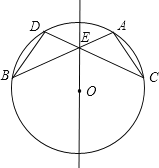
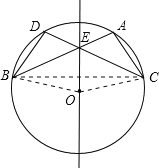
【题目】如图,在⊙O中,弦AB与DC相交于点E,AB=CD.
(1)求证:△AEC≌△DEB;
(2)点B与点C关于直线OE对称吗?试说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)要证△AEC≌△DEB,由于AB=CD,根据等弦所对的弧相等得![]() =
=![]() ,根据等量减等量还是等量,得
,根据等量减等量还是等量,得![]() =
=![]() ,由等弧对等弦得BD=CA,由圆周角定理得,∠ACE=∠DBE,∠AEC=∠DEB,即可根据AAS判定;
,由等弧对等弦得BD=CA,由圆周角定理得,∠ACE=∠DBE,∠AEC=∠DEB,即可根据AAS判定;
(2)由△AEC≌△DEB得,BE=CE,得到点E在直线BC的中垂线上,连接BO,CO,BO和CO是半径,则BO和CO相等,即点O在线段BC的中垂线上,亦即直线EO是线段BC的中垂线,所以点B与点C关于直线OE对称.
(1)证明:∵AB=CD,
∴![]() =
=![]() .
.
∴![]() -
-![]() =
=![]() -
-![]() .
.
∴![]() =
=![]() .
.
∴BD=CA.
在△AEC与△DEB中,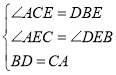 ,
,
∴△AEC≌△DEB(AAS).
(2)点B与点C关于直线OE对称.
理由如下:如图,连接OB、OC、BC.
由(1)得BE=CE.
∴点E在线段BC的中垂线上,
∵BO=CO,
∴点O在线段BC的中垂线上,
∴直线EO是线段BC的中垂线,
∴点B与点C关于直线OE对称.

练习册系列答案
相关题目