题目内容
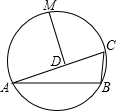 如图,已知在△ABC中,D为AC上一点,且AD=DC+CB.过D作AC的垂线交外接圆于M,求证:M为优弧
如图,已知在△ABC中,D为AC上一点,且AD=DC+CB.过D作AC的垂线交外接圆于M,求证:M为优弧 | AB |
分析:延长AC至E,使CE=BC,连MA,MB,ME,BE,由AD=DC+CB,得AD=DC+CE=DE,则∠1=∠3,而AD⊥AE,得到MA=ME;再由CE=CB,得∠2=∠5,而∠3=∠4=∠1,得到∠MBE=∠MEB,则ME=MB,于是有MA=MB,根据在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等得到M为优弧
的中点.
 |
| AB |
解答:证明:延长AC至E,使CE=BC,连MA,MB,ME,BE,如图,
∵AD=DC+CB,
∴AD=DC+CE=DE,
∴∠1=∠3,
而MD⊥AE,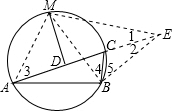
∴MA=ME;
又∵CE=CB,
∴∠2=∠5,
∵∠3=∠4=∠1,
∴∠1+∠2=∠4+∠5,
即∠MBE=∠MEB,
∴ME=MB,
∴MA=MB,
∴弧MA=弧MB,
∴M为优弧
的中点.
∵AD=DC+CB,
∴AD=DC+CE=DE,
∴∠1=∠3,
而MD⊥AE,

∴MA=ME;
又∵CE=CB,
∴∠2=∠5,
∵∠3=∠4=∠1,
∴∠1+∠2=∠4+∠5,
即∠MBE=∠MEB,
∴ME=MB,
∴MA=MB,
∴弧MA=弧MB,
∴M为优弧
 |
| AB |
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.也考查等腰三角形的判定与性质以及圆周角定理的推论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN. 如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.
如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为
如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为 如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.
如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.