题目内容
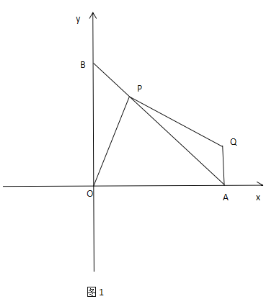
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() 经过ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,SABCD=5.
经过ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,SABCD=5.
(1)填空:点A的坐标为________;
(2)求双曲线和AB所在直线的解析式.

【答案】(1)(0,1);(2)双曲线的解析式为y=![]() , AB所在直线的解析式为y=
, AB所在直线的解析式为y=![]() x+1.
x+1.
【解析】试题(1)由D的坐标以及点A在y轴上,且AD∥x轴即可求得;
(2)由平行四边形的面积求得AE的长,即可求得OE的长,得到B的纵坐标,代入反比例函数得解析式求得B的坐标,然后根据待定系数法即可求得AB所在直线的解析式.
试题解析:(1)∵点D的坐标为(2,1),点A在y轴上,且AD∥x轴,
∴A(0,1);
(2)∵双曲线y=![]() 经过点D(2,1),
经过点D(2,1),
∴k=2×1=2,
∴双曲线为y=![]() ,
,
∵D(2,1),AD∥x轴,
∴AD=2,
∵SABCD=5,
∴AE=![]() ,
,
∴OE=![]() ,
,
∴B点纵坐标为-![]() ,
,
把y=-![]() 代入y=
代入y=![]() 得,-
得,-![]() =
=![]() ,解得x=-
,解得x=-![]() ,
,
∴B(-![]() ,-
,-![]() ),
),
设直线AB的解析式为y=ax+b,
代入A(0,1),B(-![]() ,-
,-![]() )得:
)得: ,
,
解得: ,
,
∴AB所在直线的解析式为y=![]() x+1.
x+1.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目