题目内容
如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落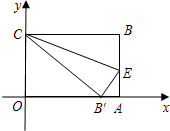 在x轴上,记为B′,折痕为CE,已知tan∠OB′C=
在x轴上,记为B′,折痕为CE,已知tan∠OB′C=| 3 | 4 |
(1)求B′点的坐标;
(2)求折痕CE所在直线的解析式.
分析:(1)由tan∠OB′C=
,OC=9,利用三角函数即可求得OB′长.
(2)易知C(0,3),由勾股定理可得B'C的长,也就求得了OA长,那么利用直角三角形AB'E就能求得AE长,进而求得E的坐标,把这两点代入一次函数解析式即可.
| 3 |
| 4 |
(2)易知C(0,3),由勾股定理可得B'C的长,也就求得了OA长,那么利用直角三角形AB'E就能求得AE长,进而求得E的坐标,把这两点代入一次函数解析式即可.
解答:解:(1)在Rt△B′OC中,tan∠OB′C=
,OC=9,
∴
=
,
解得OB′=12,
即点B′的坐标为(12,0).
(2)将纸片翻折后,点B恰好落在x轴上的B′点,CE为折痕,
∴△CBE≌△CB′E,故BE=B′E,CB′=CB=OA,
由勾股定理,得CB′=
=15,
设AE=a,则EB′=EB=9-a,AB′=AO-OB′=15-12=3,
由勾股定理,得
a2+32=(9-a)2,
解得a=4,
∴点E的坐标为(15,4),点C的坐标为(0,9),
设直线CE的解析式为y=kx+b,根据题意,得
,
解得
,
∴CE所在直线的解析式为y=-
x+9.
| 3 |
| 4 |
∴
| 9 |
| OB′ |
| 3 |
| 4 |
解得OB′=12,
即点B′的坐标为(12,0).
(2)将纸片翻折后,点B恰好落在x轴上的B′点,CE为折痕,
∴△CBE≌△CB′E,故BE=B′E,CB′=CB=OA,
由勾股定理,得CB′=
| OB′2+OC2 |
设AE=a,则EB′=EB=9-a,AB′=AO-OB′=15-12=3,
由勾股定理,得
a2+32=(9-a)2,
解得a=4,
∴点E的坐标为(15,4),点C的坐标为(0,9),
设直线CE的解析式为y=kx+b,根据题意,得
|
解得
|
∴CE所在直线的解析式为y=-
| 1 |
| 3 |
点评:矩形的对边相等,翻折前后得到的对应边相等.翻折问题一般要整理为直角三角形问题求解.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: