Question

已知一个等腰梯形的下底与上底之差等于一腰长，则这个等腰梯形中较小的角的度数为

1. A.
   75°
2. B.
   30°
3. C.
   45°
4. D.
   60°

Answer 1

D
分析：过点D作DE∥AB，交BC于点E，根据已知及等腰梯形的性质得到△DEC是等边三角形，从而得到梯形的一内角为60°．
解答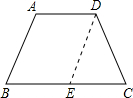：解：如图，过点D作DE∥AB，交BC于点E．
由已知知等腰梯形两底之差等于一腰的长，
故可得DC=DE，又知AB=DE，
即△DEC是等边三角形，所以∠C=60°，
故这个梯形较小内角的度数是60°，
故选D．
点评：本题主要考查等腰梯形的性质，解答本题的关键是熟练掌握等腰梯形的性质及梯形中常见的辅助线的作法，此题难度一般．