题目内容
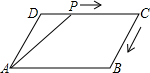 如下图,在平行四边形ABCD中,∠DAB=60°,AB=5,BC=3,点P从起点D出发,沿DC、CB向终点B匀速运动.设点P所走过的路程为x,点P所经过的线段与线段AD、AP所围成图形的面积为y,y随x的变化而变化.在下列图象中,能正确反映y与x的函数关系的是( )
如下图,在平行四边形ABCD中,∠DAB=60°,AB=5,BC=3,点P从起点D出发,沿DC、CB向终点B匀速运动.设点P所走过的路程为x,点P所经过的线段与线段AD、AP所围成图形的面积为y,y随x的变化而变化.在下列图象中,能正确反映y与x的函数关系的是( )A、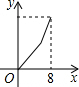 | B、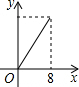 | C、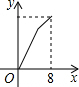 | D、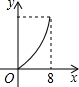 |
分析:本题考查动点函数图象的问题,先求出函数关系式在判断选项.
解答:解:当点P在CD上运动时,y为三角形,面积为:
×3×
x=
x,为正比例函数;
当点P在CB上运动时,y为梯形,面积为
×(x-5+3)×
=
,为一次函数.
由于后面的面积的x的系数>前面的x的系数,所以后面函数的图象应比前面函数图象要陡.
故选A.
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
当点P在CB上运动时,y为梯形,面积为
| 1 |
| 2 |
5
| ||
| 2 |
5
| ||||
| 4 |
由于后面的面积的x的系数>前面的x的系数,所以后面函数的图象应比前面函数图象要陡.
故选A.
点评:本题需注意的知识点是:两个在第一象限的一次函数,比例系数大的图象较陡.

练习册系列答案
相关题目
 (
(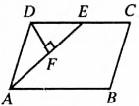 7、如下图,在平行四边形ABCD中,AE平分∠BAD交DC边于点E,DF⊥AE于F,已知∠ADF=50°,∠C的度数为( )
7、如下图,在平行四边形ABCD中,AE平分∠BAD交DC边于点E,DF⊥AE于F,已知∠ADF=50°,∠C的度数为( )