题目内容
 如图,直径12cm的圆中,弦AB把圆分成1:5两部分,C为圆上一点,∠ACB=
如图,直径12cm的圆中,弦AB把圆分成1:5两部分,C为圆上一点,∠ACB=30°
30°
.分析:首先设圆心为O,连接OA,OB,CA,CB,由弦AB把圆分成1:5两部分,可求得∠AOB的度数,然后由圆周角定理,求得答案.
解答: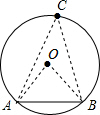 解:设圆心为O,连接OA,OB,CA,CB,
解:设圆心为O,连接OA,OB,CA,CB,
∵弦AB把圆分成1:5两部分,
∴∠AOB=
×360=60°,
∴∠ACB=
∠AOB=30°.
故答案为:30°.
 解:设圆心为O,连接OA,OB,CA,CB,
解:设圆心为O,连接OA,OB,CA,CB,∵弦AB把圆分成1:5两部分,
∴∠AOB=
| 1 |
| 6 |
∴∠ACB=
| 1 |
| 2 |
故答案为:30°.
点评:此题考查了圆周角定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
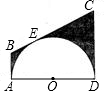 如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
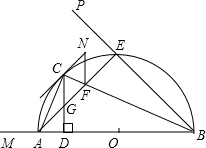 N∥CD,过C作圆的切线交FN于N.
N∥CD,过C作圆的切线交FN于N.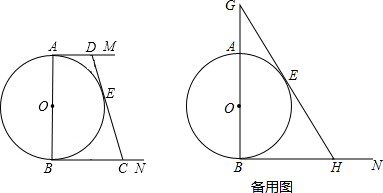
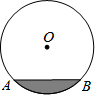 如图,直径为20cm,截面为圆的水槽⊙O中有一些水,此时水面宽AB=12cm,后来水面上升了一定距离,但仍没有超过圆心,此时水面宽AB=16cm,则水面上升了
如图,直径为20cm,截面为圆的水槽⊙O中有一些水,此时水面宽AB=12cm,后来水面上升了一定距离,但仍没有超过圆心,此时水面宽AB=16cm,则水面上升了