题目内容
小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关。因此,他们认为:可以借助物体的影子长度计算光源到物体的位置,于是,他们做了以下尝试
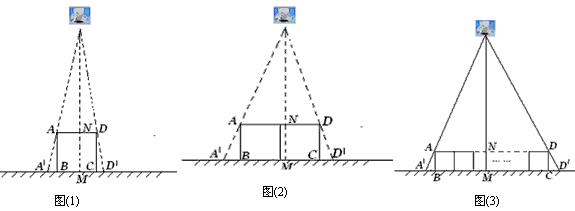
(1) 如图(1),垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B与D′C的长度和为6cm.那么灯泡离地面的高度为_____;
(2)不改变(1)中灯泡的高度,将两个边长为30cm的正方形框架按图(2)摆放,请计算此时横向影子A′B与D′C的长度和为多少?
(3)有n个边长为a的正方形按图(3)摆放,测得横向影子A′B与D′C的长度和为 b,求灯泡离地面的距离(写出解题过程,结果用含a,b,n的代数式表示)
(1) 如图(1),垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B与D′C的长度和为6cm.那么灯泡离地面的高度为_____;
(2)不改变(1)中灯泡的高度,将两个边长为30cm的正方形框架按图(2)摆放,请计算此时横向影子A′B与D′C的长度和为多少?
(3)有n个边长为a的正方形按图(3)摆放,测得横向影子A′B与D′C的长度和为 b,求灯泡离地面的距离(写出解题过程,结果用含a,b,n的代数式表示)
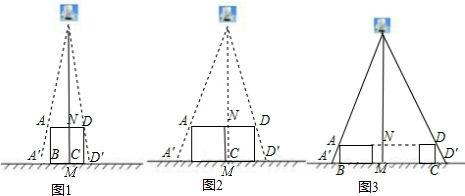
| (1)180cm. (2)12 cm. (3)记灯泡为点P,如图 ∵AD∥A′D′, ∴∠PAD=∠PA′D′,∠PDA=∠P D′A′. ∴△PAD∽△PA′D′. 根据相似三角形对应高的比等于相似比的性质, 可得 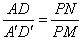 . .设灯泡离地面距离为x 由题意,得 PM=x,PN=x-a,AD= na,A′D′=  , , ∴ 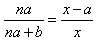 解得: 解得: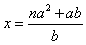 . .所以灯泡离地面的距离为 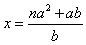 |
 |

练习册系列答案
相关题目

 (2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少? (2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?