ΧβΡΩΡΎ»ί
“―÷ΣΕΰ¥ΈΚ· ΐy=(t+1)x2+2(t+2)x+ Θ§‘Ύx=0ΚΆx=2 ±ΒΡΚ· ΐ÷ΒœύΒ»ΓΘ
Θ§‘Ύx=0ΚΆx=2 ±ΒΡΚ· ΐ÷ΒœύΒ»ΓΘ
Θ®1Θ©«σΕΰ¥ΈΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©»τ“Μ¥ΈΚ· ΐy=kx+6ΒΡΆΦœώ”κΕΰ¥ΈΚ· ΐΒΡΆΦœώΕΦΨ≠ΙΐΒψAΘ®-3Θ§mΘ©Θ§«σmΚΆkΒΡ÷ΒΘΜ
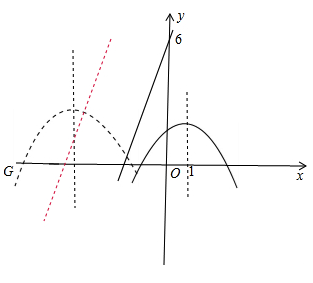
Θ®3Θ©…ηΕΰ¥ΈΚ· ΐΒΡΆΦœσ”κx÷αΫΜ”ΎΒψBΘ§CΘ®ΒψC‘ΎΒψBΘ§CΒΡΉσ≤ύΘ©Θ§ΫΪΕΰ¥ΈΚ· ΐΒΡΆΦœσ‘ΎΒψBΘ§CΦδΒΡ≤ΩΖ÷Θ®Κ§ΒψCΚΆΒψCΘ©œρΉσΤΫ“Τn(n>0)ΗωΒΞΈΜΚσΒΟΒΫΒΡΆΦœσΦ«ΈΣGΘ§Ά§ ±ΫΪΘ®2Θ©÷–ΒΟΒΫΒΡ÷±œΏy=kx+6œρ…œΤΫ“ΤnΗωΒΞΈΜΓΘ«κΫαΚœΆΦœσΜΊ¥πΘΚΒ±ΤΫ“ΤΚσΒΡ÷±œΏ”κΆΦœσG”–ΙΪΙ≤Βψ ±Θ§nΒΡ»Γ÷ΒΖΕΈßΓΘ
 Θ§‘Ύx=0ΚΆx=2 ±ΒΡΚ· ΐ÷ΒœύΒ»ΓΘ
Θ§‘Ύx=0ΚΆx=2 ±ΒΡΚ· ΐ÷ΒœύΒ»ΓΘΘ®1Θ©«σΕΰ¥ΈΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©»τ“Μ¥ΈΚ· ΐy=kx+6ΒΡΆΦœώ”κΕΰ¥ΈΚ· ΐΒΡΆΦœώΕΦΨ≠ΙΐΒψAΘ®-3Θ§mΘ©Θ§«σmΚΆkΒΡ÷ΒΘΜ
Θ®3Θ©…ηΕΰ¥ΈΚ· ΐΒΡΆΦœσ”κx÷αΫΜ”ΎΒψBΘ§CΘ®ΒψC‘ΎΒψBΘ§CΒΡΉσ≤ύΘ©Θ§ΫΪΕΰ¥ΈΚ· ΐΒΡΆΦœσ‘ΎΒψBΘ§CΦδΒΡ≤ΩΖ÷Θ®Κ§ΒψCΚΆΒψCΘ©œρΉσΤΫ“Τn(n>0)ΗωΒΞΈΜΚσΒΟΒΫΒΡΆΦœσΦ«ΈΣGΘ§Ά§ ±ΫΪΘ®2Θ©÷–ΒΟΒΫΒΡ÷±œΏy=kx+6œρ…œΤΫ“ΤnΗωΒΞΈΜΓΘ«κΫαΚœΆΦœσΜΊ¥πΘΚΒ±ΤΫ“ΤΚσΒΡ÷±œΏ”κΆΦœσG”–ΙΪΙ≤Βψ ±Θ§nΒΡ»Γ÷ΒΖΕΈßΓΘ
ΫβΘΚ(1)”…Χβ“βΩ…÷Σ“άΕΰ¥ΈΚ· ΐΆΦœσΒΡΕ‘≥Τ÷αΈΣ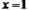 ‘ρ 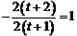 ΓΘ ΓΘΓύ 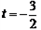 Γύ 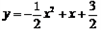 (2)ΓΏ“ρΕΰ¥ΈΚ· ΐΆΦœσ±ΊΨ≠Ιΐ 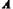 Βψ ΒψΓύ   ”÷“Μ¥ΈΚ· ΐ ”÷“Μ¥ΈΚ· ΐ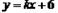 ΒΡΆΦœσΨ≠Ιΐ ΒΡΆΦœσΨ≠Ιΐ Βψ ΒψΓύ 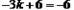 Θ§ Θ§Γύ  (3) ”…Χβ“βΩ…÷ΣΘ§Βψ 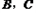 ΦδΒΡ≤ΩΖ÷ΆΦœσΒΡΫβΈω ΫΈΣ ΦδΒΡ≤ΩΖ÷ΆΦœσΒΡΫβΈω ΫΈΣ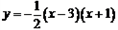 Θ§ Θ§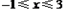 ‘ρœρΉσΤΫ“ΤΚσΒΟΒΫΒΡΆΦœσ 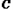 ΒΡΫβΈω ΫΈΣ ΒΡΫβΈω ΫΈΣ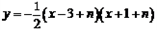 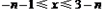 ¥Υ ±ΤΫ“ΤΚσΒΡΫβΈω ΫΈΣ 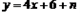 ”…ΆΦœσΩ…÷ΣΘ§ ”…ΆΦœσΩ…÷ΣΘ§ΤΫ“ΤΚσΒΡ÷±œΏ”κΆΦœσ  ”–ΙΪΙ≤ΒψΘ§‘ρΝΫΗωΝΌΫγΒΡΫΜΒψΈΣ ”–ΙΪΙ≤ΒψΘ§‘ρΝΫΗωΝΌΫγΒΡΫΜΒψΈΣ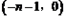 ”κ ”κ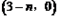 ‘ρ 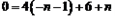 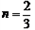 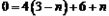  Γύ 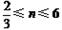 |
 |

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 Θ®2013•ήλΡœœΊΕΰΡΘΘ©“―÷ΣΕΰ¥ΈΚ· ΐy=ax2+bx+cΘ®aΓΌ0Θ©ΒΡΆΦœσ»γΆΦΥυ ΨΘ§”–œ¬Ν–5ΗωΫα¬έΘΚ
Θ®2013•ήλΡœœΊΕΰΡΘΘ©“―÷ΣΕΰ¥ΈΚ· ΐy=ax2+bx+cΘ®aΓΌ0Θ©ΒΡΆΦœσ»γΆΦΥυ ΨΘ§”–œ¬Ν–5ΗωΫα¬έΘΚ “―÷ΣΕΰ¥ΈΚ· ΐy=ax2+bx+cΘ®aΓΌ0Θ©ΒΡΆΦœσ»γΆΦΥυ ΨΘ§‘ρœ¬Ν–Ϋα¬έΘΚΔΌacΘΨ0ΘΜΔΎa-b+cΘΦ0ΘΜ
“―÷ΣΕΰ¥ΈΚ· ΐy=ax2+bx+cΘ®aΓΌ0Θ©ΒΡΆΦœσ»γΆΦΥυ ΨΘ§‘ρœ¬Ν–Ϋα¬έΘΚΔΌacΘΨ0ΘΜΔΎa-b+cΘΦ0ΘΜ