题目内容
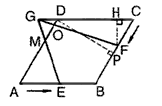
如图所示,菱形ABCD的边长为6cm,∠DAB=60°,点M是边AD上一点,且DM=2cm,点E、F分别从A、C同时出发,以1cm/s的速度分别沿边AB、CB向点B运动,EM、CD的延长线相交于G,GF交AD于O。设运动时间为x(s),△CGF的面积为y(cm2)。
(1)当x为何值时,GD的长度是2cm?
(2)求y与x之间的函数关系式;
(3)是否存在某一时刻,使得线段GF把菱形ABCD分成的上、下两部分的面积之比为1:5?若存在,求出此时x的值;若不存在,说明理由。
(1)当x为何值时,GD的长度是2cm?
(2)求y与x之间的函数关系式;
(3)是否存在某一时刻,使得线段GF把菱形ABCD分成的上、下两部分的面积之比为1:5?若存在,求出此时x的值;若不存在,说明理由。

| 解:(1)∵DC∥AB, ∴△DMG∽△AME, ∴  ∴ 即当x=4s时,GD的长度是2cm; (2)∵△DMG∽△AME ∴ 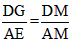 ∴ 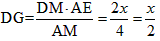 ∴GC= 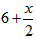 , ,过F作FH⊥DC于H点 ∴FH= 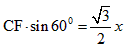 ∴ 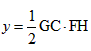 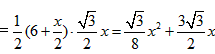 ; ;(3)设运动x(s)时,GF分菱形上、下两部分的面积比为1:5 此时△OGD∽△FGC, ∴ 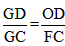 ∴ 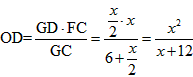 , ,过D作DP⊥BC于P,则PD=6×sin60°= 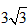 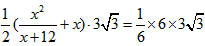 即 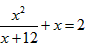 解得: 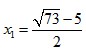 , ,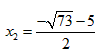 (舍去) (舍去) 经检验: 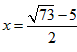 是原方程的解, 是原方程的解,∴当  时,GF分菱形上、下两部分的面积比为1:5。 时,GF分菱形上、下两部分的面积比为1:5。 |
 |

练习册系列答案
相关题目
 23、如图所示,在△ABC中,AD⊥BC于点D,E,F分别是AB,AC边的中点,连接DE,EF,FD,当△ABC满足条件
23、如图所示,在△ABC中,AD⊥BC于点D,E,F分别是AB,AC边的中点,连接DE,EF,FD,当△ABC满足条件 30、如图所示,以△ABC的三边为边,分别作三个等边三角形.
30、如图所示,以△ABC的三边为边,分别作三个等边三角形.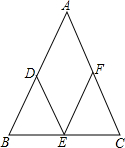 已知:如图所示,在△ABC中,D、E、F分别是AB、BC、AC边上的中点.
已知:如图所示,在△ABC中,D、E、F分别是AB、BC、AC边上的中点. 49、如图所示,在△ABC中,AB=AC,P为BC的中点,PE⊥AB于E,PF⊥AC于F,EM⊥AC于M,FN⊥AB于N,EM与FN相交于点Q,那么四边形PEQF是菱形吗?说明你的理由.
49、如图所示,在△ABC中,AB=AC,P为BC的中点,PE⊥AB于E,PF⊥AC于F,EM⊥AC于M,FN⊥AB于N,EM与FN相交于点Q,那么四边形PEQF是菱形吗?说明你的理由. 26、如图所示,Rt△ABC中,∠BAC=Rt∠,AD⊥BC于点D,∠ABC的平分线交AD于O,交AC于E,OG∥AC交BC于G.
26、如图所示,Rt△ABC中,∠BAC=Rt∠,AD⊥BC于点D,∠ABC的平分线交AD于O,交AC于E,OG∥AC交BC于G.