题目内容
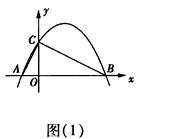
已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点在y 轴正半轴上(如图(1))。
(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式;
(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式;
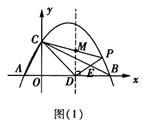
(2)如图(2),点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E。
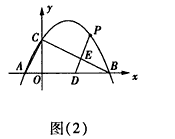
①当△BDE是等腰三角形时,直接写出此时点E的坐标;
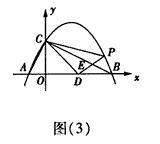
②又连接CD、CP(如图(3)),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由。
②又连接CD、CP(如图(3)),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由。
| 解:(1)∵OC2=OA·OB, ∴OA·OB=4, 又∵OA+OB=5,且OA<OB, 解得,OA=1,OB=4, ∴A(-1,0),B(4,0),C(0,2), 设过A、B、C三点的抛物线的解析式为:y=a(x+1)(x-4), 把C点坐标代入得 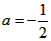 , , ∴ 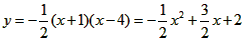 ; ; |
|
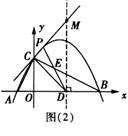
(2)①当△BDE为等腰三角形时,点E的坐标分别为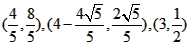 , ,②存在,过点D作直线DM垂直于x轴交CP于点M, 可求得直线CP的解析式为:y= 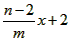 ; ;(i)当点P在直线DM右侧时,如图(1)所示, 此时2<m<4, 把x=2代人直线CP的解析式 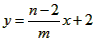 , ,得 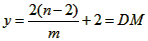 又P(m,n)在抛物线上, 所以 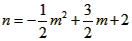 S △CDP= S△PDM +S△CDM 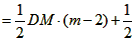 DM·2=  ·DM=m+n-2, ·DM=m+n-2,即  当 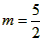 时,△CDP的面积最大,最大面积为 时,△CDP的面积最大,最大面积为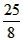 ; ;(ii)当点P在直线DM左侧时,如图(2)所示,此时0<m≤2, S△CDP= S△CDM - S△DPM 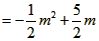 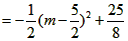 , ,当m=2时,S△CDP=3, 综上所述,当 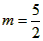 时△CDP的面积最大,其最大面积为 时△CDP的面积最大,其最大面积为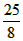 ,此时 ,此时 。 。 |
  |

练习册系列答案
相关题目
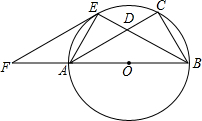 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.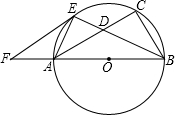 ∥AC交BA的延长线于F.
∥AC交BA的延长线于F.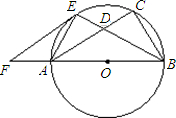 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交
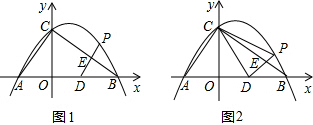 已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上,点D的坐标为(2,0).
已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上,点D的坐标为(2,0).