Question

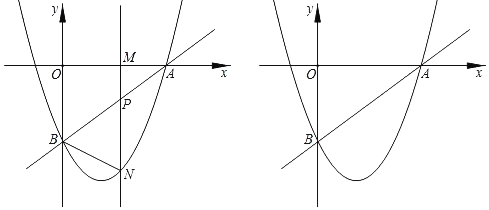
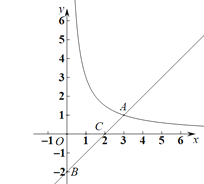
【题目】如图，在平面直角坐标系中，函数的图像与直线交于点，直线分别交x轴，y轴于C、B两点．

（1）求的值；

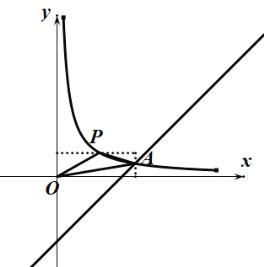
（2）已知点，当点P在函数的图像上时，求△POA的面积；

（3）点Q在函数的图像上滑动，现有以Q点为圆心，为半径的⊙Q，当⊙Q与直线相切时，求点Q的坐标．

Answer 1

【答案】（1）k=3，m=1；（2）；（3）(，)或(，)

【解析】

（1）将点A代入一次函数的解析式中即可求出m的值，进而可求出点A的坐标，然后将点A代入反比例函数中，即可求出k的值；

（2）根据反比例函数的解析式，求出点P的坐标，然后利用矩形的面积减去三个直角三角形的面积即可得到△POA的面积；

（3）先通过直线求出点B,C的坐标，进而通过OB=OC得出，然后分两种情况：当⊙Q在直线左侧与直线 相切时和当⊙Q在直线右侧与直线 相切时，作QM∥x轴交直线于点M，QN⊥直线于点N，通过特殊角的三角函数值求出Q,M的横坐标之差为2，然后设出Q,M的坐标，建立方程即可求解．

（1）∵点在直线上，

∴，

∴．

∵点在上，

；

（2）∵点P在函数的图像上，

∴ ,

∴或 （舍去）,

∴

;

（3）当时， ,

∴ ．

当时， ，解得 ,

∴ ,

，

∴ ．

当⊙Q在直线左侧与直线 相切时，作QM∥x轴交直线于点M，QN⊥直线于点N，

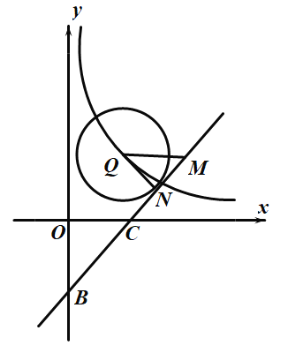
∵QM∥x轴，

∴ ．

，

．

设点 ，则

则有 ，

解得或 （舍去），

当时， ,

∴此时；

同理，当⊙Q在直线右侧与直线 相切时，则有

，

解得或 （舍去），

当时， ，

∴此时，

综上所述，Q的坐标为或