题目内容
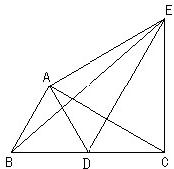11、如图，将30°的直角三角尺ABC绕直角顶点A逆时针旋转到ADE的位置，使B点的对应点D落在BC边上，连接EB、EC，则下列结论：①∠DAC=∠DCA；②ED为AC的垂直平分线；③EB平分∠AED；④ED=2AB．其中正确的是（ ）分析：根据直角三角形中30°的角所对的直角边等于斜边的一半，以及旋转的性质即可判断．
解答：解：①根据旋转的性质可以得到：AB=AD，而∠ABD=60°，则△ABD是等边三角形，可得到∠DAC=30°，∴∠DAC=∠DCA，故正确；
②根据①可得AD=CD，并且根据旋转的性质可得：AC=AE，∠EAC=60°，则△ACE是等边三角形，则EA=EC，即D、E都到AC两端的距离相等，则DE在AC的垂直平分线上，故正确；
③根据条件AB∥DE，而AB≠AE，即可证得EB平分∠AED不正确，故错误；
④根据旋转的性质，DE=BC，而BC=2AB，即可证得ED=2AB，故正确；
故正确的是：①②④．故选B．
②根据①可得AD=CD，并且根据旋转的性质可得：AC=AE，∠EAC=60°，则△ACE是等边三角形，则EA=EC，即D、E都到AC两端的距离相等，则DE在AC的垂直平分线上，故正确；
③根据条件AB∥DE，而AB≠AE，即可证得EB平分∠AED不正确，故错误；
④根据旋转的性质，DE=BC，而BC=2AB，即可证得ED=2AB，故正确；
故正确的是：①②④．故选B．
点评：正确理解旋转的性质，图形旋转前后两个图形全等是解决本题的关键．
练习册系列答案
相关题目
8、如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=50°，则∠3的度数等于（ ）
如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠3=20°，则∠2的度数等于（ ）
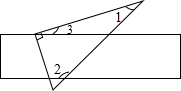如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=114°，则∠3的度数为（ ）| A、26° | B、34° | C、44° | D、36° |
如图，将30°的直角三角尺ABC绕直角顶点A逆时针旋转到ADE的位置，使B点的对应点D落在BC边上，连接EB、EC，则下列结论：①∠DAC=∠DCA；②ED为AC的垂直平分线；③EB平分∠AED；④ED=2AB．其中正确的是