题目内容
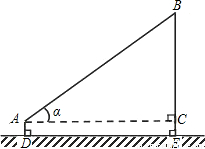
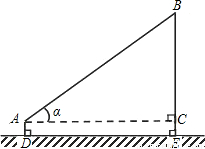
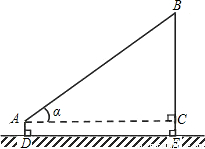
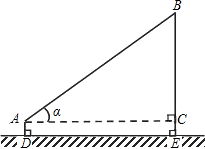 如图,小王在操场上放风筝,已知风筝线AB长100米,风筝线与水平线的夹角α=36°,小王拿风筝线的手离地面的高度AD为1.5米,求风筝离地面的高度BE(精确到0.1米).
如图,小王在操场上放风筝,已知风筝线AB长100米,风筝线与水平线的夹角α=36°,小王拿风筝线的手离地面的高度AD为1.5米,求风筝离地面的高度BE(精确到0.1米).
解:在Rt△ABC中,∠BAC=∠α=36°,AB=100米.
∵sinα= .
.
∴BC=AB•sinα=100×sin36°≈100×0.5878=58.78(米).
又∵CE=AD=1.5米.
∴BE=BC+CE=58.78+1.5=60.28≈60.3(米).
答:风筝离地面的高度BE约为60.3米.
分析:本题是一个直角梯形的问题,可以通过点C作CD⊥AB于点D,把求AB的问题转化求AD的长,从而可以在△ACB中利用三角函数.
点评:解直角梯形可以通过作高线转化为解直角三角形和矩形的问题.
∵sinα=
 .
.∴BC=AB•sinα=100×sin36°≈100×0.5878=58.78(米).
又∵CE=AD=1.5米.
∴BE=BC+CE=58.78+1.5=60.28≈60.3(米).
答:风筝离地面的高度BE约为60.3米.
分析:本题是一个直角梯形的问题,可以通过点C作CD⊥AB于点D,把求AB的问题转化求AD的长,从而可以在△ACB中利用三角函数.
点评:解直角梯形可以通过作高线转化为解直角三角形和矩形的问题.

练习册系列答案
相关题目
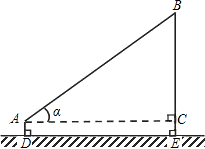 如图,小王在操场上放风筝,已知风筝线AB长100米,风筝线与水平线的夹角α=36°,小王拿风筝线的手离地面的高度AD为1.5米,求风筝离地面的高度BE(精确到0.1米).
如图,小王在操场上放风筝,已知风筝线AB长100米,风筝线与水平线的夹角α=36°,小王拿风筝线的手离地面的高度AD为1.5米,求风筝离地面的高度BE(精确到0.1米).