��Ŀ����
��֪���ڡ�ABC�У���BAC=90�㣬��ABC=45�㣬��DΪֱ��BC��һ���㣨��D�����B��C�غϣ�����ADΪ����������ADEF������CF
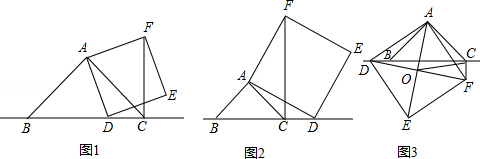
��1����ͼ1������D���߶�BC��ʱ����֤CF+CD=BC��
��2����ͼ2������D���߶�BC���ӳ�����ʱ�������������䣬��ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ��
��3����ͼ3������D���߶�BC�ķ����ӳ�����ʱ���ҵ�A��F�ֱ���ֱ��BC�����࣬�����������䣻
����ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ��
����������ADEF�ı߳�Ϊ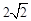 ���Խ���AE��DF�ཻ�ڵ�O������OC����OC�ij��ȣ�
���Խ���AE��DF�ཻ�ڵ�O������OC����OC�ij��ȣ�

��1����ͼ1������D���߶�BC��ʱ����֤CF+CD=BC��
��2����ͼ2������D���߶�BC���ӳ�����ʱ�������������䣬��ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ��
��3����ͼ3������D���߶�BC�ķ����ӳ�����ʱ���ҵ�A��F�ֱ���ֱ��BC�����࣬�����������䣻
����ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ��
����������ADEF�ı߳�Ϊ
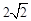 ���Խ���AE��DF�ཻ�ڵ�O������OC����OC�ij��ȣ�
���Խ���AE��DF�ཻ�ڵ�O������OC����OC�ij��ȣ��⣺��1��֤�����ߡ�BAC=90�㣬��ABC=45�㣬���ACB=��ABC=45�㡣��AB=AC��
���ı���ADEF�������Σ���AD=AF����DAF=90�㡣
�ߡ�BAD=90�㩁��DAC����CAF=90�㩁��DAC�����BAD=��CAF��
���ڡ�BAD�͡�CAF�У�AB=AC����BAD=��CAF��AD=AF��
���BAD�ա�CAF��SAS������BD=CF��
��BD+CD=BC����CF+CD=BC��
��2��CF��CD=BC��
��3����CD��CF=BC��
�ڡߡ�BAC=90�㣬��ABC=45�㣬���ACB=��ABC=45�㡣��AB=AC��
���ı���ADEF�������Σ���AD=AF����DAF=90�㡣
�ߡ�BAD=90�㩁��BAF����CAF=90�㩁��BAF�����BAD=��CAF��
���ڡ�BAD�͡�CAF�У�AB=AC����BAD=��CAF��AD=AF��
���BAD�ա�CAF��SAS�������ACF=��ABD��
�ߡ�ABC=45�㣬���ABD=135�㡣���ACF=��ABD=135�㡣���FCD=90�㡣
���FCD��ֱ�������Ρ�
��������ADEF�ı߳�Ϊ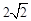 �ҶԽ���AE��DF�ཻ�ڵ�O��
�ҶԽ���AE��DF�ཻ�ڵ�O��
��DF=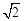 AD=4��OΪDF�е㡣
AD=4��OΪDF�е㡣
��OC= DF=2��
DF=2��
���ı���ADEF�������Σ���AD=AF����DAF=90�㡣
�ߡ�BAD=90�㩁��DAC����CAF=90�㩁��DAC�����BAD=��CAF��
���ڡ�BAD�͡�CAF�У�AB=AC����BAD=��CAF��AD=AF��
���BAD�ա�CAF��SAS������BD=CF��
��BD+CD=BC����CF+CD=BC��
��2��CF��CD=BC��
��3����CD��CF=BC��
�ڡߡ�BAC=90�㣬��ABC=45�㣬���ACB=��ABC=45�㡣��AB=AC��
���ı���ADEF�������Σ���AD=AF����DAF=90�㡣
�ߡ�BAD=90�㩁��BAF����CAF=90�㩁��BAF�����BAD=��CAF��
���ڡ�BAD�͡�CAF�У�AB=AC����BAD=��CAF��AD=AF��
���BAD�ա�CAF��SAS�������ACF=��ABD��
�ߡ�ABC=45�㣬���ABD=135�㡣���ACF=��ABD=135�㡣���FCD=90�㡣
���FCD��ֱ�������Ρ�
��������ADEF�ı߳�Ϊ
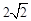 �ҶԽ���AE��DF�ཻ�ڵ�O��
�ҶԽ���AE��DF�ཻ�ڵ�O����DF=
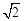 AD=4��OΪDF�е㡣
AD=4��OΪDF�е㡣��OC=
 DF=2��
DF=2�������������1��������ABC�ǵ���ֱ�������Σ�����SAS����֤����BAD�ա�CAF���Ӷ�֤��CF=BD���ݴ˼���֤�á�
��2��ͬ��1����ͬ������SAS����֤�á�BAD�ա�CAF���Ӷ�֤��BD=CF�����ɵõ�CF��CD=BC��
��3����ͬ��1����ͬ������SAS����֤�á�BAD�ա�CAF���Ӷ�֤��BD=CF�����ɵõ�CD��CF=BC��
��֤����BAD�ա�CAF����FCD��ֱ�������Σ�Ȼ����������ε����ʼ������DF�ij�����OC������á���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ