题目内容
如图所示,等腰梯形ABCD,AB∥DC,AD=AB=BC=2,CD=4,有两个动点P、Q,同时从D点出发,点P沿D-A-B-C以每秒2个单位长度的速度移动,点Q沿线段DC以每秒1个单位长度的速度移动,当点P、Q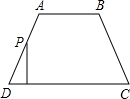 有一个点到达点C时,另一点也停止移动,若移动的时间为t秒,△DPQ的面积为S个平方单位.
有一个点到达点C时,另一点也停止移动,若移动的时间为t秒,△DPQ的面积为S个平方单位.(1)直接写出S与t的函数关系式:
(2)当t为何值时S取最大值,最大值为多少?
(3)在运动过程中,是否存在某一时刻t,使直线PQ与等腰梯形ABCD的某一边所夹的锐角等于30°?若存在,直接写出t的范围或t的值;若不存在,说明理由.
分析:(1)根据等边三角形的性质求出∠D=60°,根据勾股定理求出梯形的高
,有3种情况:①0<t≤1时,根据三角形的面积公式求出即可;②1<t≤2时,根据三角形的面积公式求出即可;③当2<t<3时,根据三角形的面积求出即可;
(2)通过计算得出只有t=2时,S有最大值,把t=2代入即可求出答案;
(3)当P在AD上时,∠DPQ=30°,即可求出t的范围;当P在BC上时,∠PQC=30°,根据直角三角形的性质求出即可.
| 3 |
(2)通过计算得出只有t=2时,S有最大值,把t=2代入即可求出答案;
(3)当P在AD上时,∠DPQ=30°,即可求出t的范围;当P在BC上时,∠PQC=30°,根据直角三角形的性质求出即可.
解答:解:(1)S与t的函数关系式是S=
t2(0<t≤1),S=
t(1<t≤2),S=-
t2+
t(2<<3).
(2)当t=2时,S有最大值,最大值是S=
t=
,
答:t为2时S取最大值,最大值为
.
(3)存在,t的范围是0<t≤1 或t=
.
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
(2)当t=2时,S有最大值,最大值是S=
| ||
| 2 |
| 3 |
答:t为2时S取最大值,最大值为
| 3 |
(3)存在,t的范围是0<t≤1 或t=
| 8 |
| 3 |
点评:本题主要考查对等腰梯形的性质,二次函数的最值,等边三角形的性质和判定,勾股定理,含30度角的直角三角形性质,三角形的内角和定理,三角形的面积等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,等腰梯形ABCD中,DC∥AB,对角线AC与BD交于点O,AD=DC,AC=BD=AB.
如图所示,等腰梯形ABCD中,DC∥AB,对角线AC与BD交于点O,AD=DC,AC=BD=AB.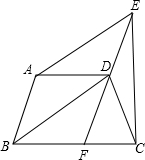 如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点.
如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点. 20、现有5张如图所示的等腰梯形纸片,打算用其中的若干张来拼成较大的等腰梯形,你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.
20、现有5张如图所示的等腰梯形纸片,打算用其中的若干张来拼成较大的等腰梯形,你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长. 如图所示,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,延长BC至点E,使得CE=AD
如图所示,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,延长BC至点E,使得CE=AD 已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,
已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,