题目内容
【题目】如图,抛物线![]() 与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:
与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:![]() 与y轴交于点C,与抛物线
与y轴交于点C,与抛物线![]() 的另一个交点为D,已知
的另一个交点为D,已知![]() ,P点为抛物线
,P点为抛物线![]() 上一动点(不与A、D重合).
上一动点(不与A、D重合).
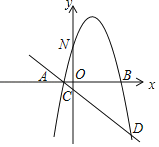
(1)求抛物线和直线l的解析式;
(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作![]() 轴交直线l于点F,求
轴交直线l于点F,求![]() 的最大值;
的最大值;
(3)设M为直线l上的点,探究是否存在点M,使得以点N、C,M、P为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ,直线l的表达式为:
,直线l的表达式为:![]() ;(2)
;(2)![]() 最大值:18;(3)存在,P的坐标为:
最大值:18;(3)存在,P的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将点A、D的坐标分别代入直线表达式、抛物线的表达式,即可求解;
(2)![]() ,即可求解;
,即可求解;
(3)分NC是平行四边形的一条边、NC是平行四边形的对角线,两种情况分别求解即可.
解:(1)将点A、D的坐标代入直线表达式得:![]() ,解得:
,解得:![]() ,
,
故直线l的表达式为:![]() ,
,
将点A、D的坐标代入抛物线表达式,
同理可得抛物线的表达式为:![]() ;
;
(2)直线l的表达式为:![]() ,则直线l与x轴的夹角为
,则直线l与x轴的夹角为![]() ,
,
即:则![]() ,
,

设点P坐标为![]() 、则点
、则点![]() ,
,
![]()
![]() ,故
,故![]() 有最大值,
有最大值,
当![]() 时,其最大值为18;
时,其最大值为18;
(3)![]() ,
,
①当NC是平行四边形的一条边时,
设点P坐标为![]() 、则点
、则点![]() ,
,
由题意得:![]() ,即:
,即:![]() ,
,
解得![]() 或0或4(舍去0),
或0或4(舍去0),
则点P坐标为![]() 或
或![]() 或
或![]() ;
;
②当NC是平行四边形的对角线时,
则NC的中点坐标为![]() ,
,
设点P坐标为![]() 、则点
、则点![]() ,
,
N、C,M、P为顶点的四边形为平行四边形,则NC的中点即为PM中点,
即:![]() ,
,
解得:![]() 或
或![]() (舍去0),
(舍去0),
故点![]() ;
;
故点P的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案【题目】在画二次函数![]() 的图象时,甲写错了一次项的系数,列表如下
的图象时,甲写错了一次项的系数,列表如下
| …… | ﹣1 | 0 | 1 | 2 | 3 | …… |
| …… | 6 | 3 | 2 | 3 | 6 | …… |
乙写错了常数项,列表如下:
| …… | ﹣1 | 0 | 1 | 2 | 3 | …… |
| …… | ﹣2 | ﹣1 | 2 | 7 | 14 | …… |
通过上述信息,解决以下问题:
(1)求原二次函数![]() 的表达式;
的表达式;
(2)对于二次函数![]() ,当
,当![]() _____时,
_____时,![]() 的值随
的值随![]() 的值增大而增大;
的值增大而增大;
(3)若关于![]() 的方程
的方程![]() 有两个不相等的实数根,求
有两个不相等的实数根,求![]() 的取值范围.
的取值范围.