题目内容
如图,点A、O、B三点在一条直线上,C为直线AB外任意一点,OE、OF分别是∠AOC和∠BOC 的平分线.
的平分线.
(1)你能求出∠EOF的度数吗?如果能,请直接写出∠EOF的度数;
(2)写出∠COF的所有余角;
(3)写出∠AOF的所有补角.
解:(1)∵OE、OF分别是∠AOC和∠BOC的平分线.
∴∠BOF=∠COF,∠AOE=COE,
又∵∠AOC+∠BOC=180°,
∴∠AOE+∠COE+∠BOF+∠COF=180°,
∴∠EOC+∠COF=90°,
又∵∠EOF=∠EOC+∠EOF,
∴∠EOF=90°;
(2)由(1)可知,∠COF的余角有∠EOC,∠AOE;
(3)∠AOF的补角有∠BOF、∠COF.
分析:(1)由角平分线的性质得出∠BOF=∠COF,∠AOE=COE,再根据余角和补角的定义、性质求得答案即可;
(2)(3)由∠EOF=90°,根据等角的补角相等.等角的余角相等直接求出答案即可.
点评:本题考查了余角和补角的定义以及性质、角平分线的性质,若两个角的和为90°,则这两个角互余;若两个角的和等于180°,则这两个角互补.等角的补角相等.等角的余角相等.
∴∠BOF=∠COF,∠AOE=COE,
又∵∠AOC+∠BOC=180°,
∴∠AOE+∠COE+∠BOF+∠COF=180°,
∴∠EOC+∠COF=90°,
又∵∠EOF=∠EOC+∠EOF,
∴∠EOF=90°;
(2)由(1)可知,∠COF的余角有∠EOC,∠AOE;
(3)∠AOF的补角有∠BOF、∠COF.
分析:(1)由角平分线的性质得出∠BOF=∠COF,∠AOE=COE,再根据余角和补角的定义、性质求得答案即可;
(2)(3)由∠EOF=90°,根据等角的补角相等.等角的余角相等直接求出答案即可.
点评:本题考查了余角和补角的定义以及性质、角平分线的性质,若两个角的和为90°,则这两个角互余;若两个角的和等于180°,则这两个角互补.等角的补角相等.等角的余角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 24、如图,点A、O、B三点在一条直线上,C为直线AB外任意一点,OE、OF分别是∠AOC和∠BOC的平分线.
24、如图,点A、O、B三点在一条直线上,C为直线AB外任意一点,OE、OF分别是∠AOC和∠BOC的平分线.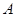 、
、 、
、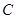 是
是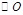 上的三点,
上的三点,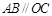 .
.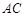 平分
平分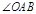 .
. 【小题2】过点
【小题2】过点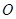 作
作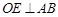 于点
于点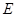 ,交
,交 于点
于点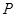 . 若
. 若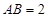 ,
, ,求
,求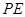 的长.
的长. 、
、 、
、 是
是 上的三点,
上的三点, .
. 平分
平分 .
. 2.过点
2.过点 作
作 于点
于点 ,交
,交 于点
于点 . 若
. 若 ,
, ,求
,求 的长.
的长.