��Ŀ����
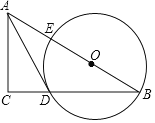
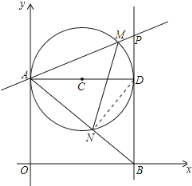
����Ŀ����ͼ����һ�����ڰ뾶Ϊ2�ġ�C��y�������ڵ�A����ֱ��AD������D����C������l��x���ڵ�B��PΪֱ��l��һ���㣬��ֱ֪��PA�Ľ���ʽΪ��y��kx+3��
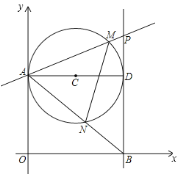
��1�����P��������Ϊp��д��p��k�仯�ĺ�����ϵʽ��
��2�����C��PA���ڵ�M����AB���ڵ�N�����۶���P����ֱ��l�ϣ�����B���⣩��ʲôλ��ʱ��������AMN�ס�ABP��������ڵ�P����ͼ��λ��ʱ�������������Ƹ���֤����
��3���Ƿ����ʹ��AMN���������![]() ��kֵ�������ڣ���������ϵ�kֵ���������ڣ���˵�����ɣ�
��kֵ�������ڣ���������ϵ�kֵ���������ڣ���˵�����ɣ�
���𰸡�(1) p��4k+3��(2)������;(3) ���ڣ�k��2��![]() ��k����2ʱ����AMN���������
��k����2ʱ����AMN���������![]() ,���ɼ�����
,���ɼ�����
��������
��1�������ߵ�����֪��AOB����OAD����ADB��90�㣬���Կ����ж��ı���OADB�Ǿ��Σ����ݡ�O�İ뾶��2���ֱ��AD��4���Ӷ���õ�P�����꣬�������ֱ�߷���y��kx��3����֪p�仯�ĺ�����ϵʽ��
��2������DN����ֱ�����Ե�Բ�ܽ���ֱ�ǣ����AND��90�㣬����ͼʾ��֤��AND����ABD��Ȼ�����ͬ�����Ե�Բ�ܽ������֪��ADN����AMN�����ɵ���������֪��ABD����AMN������������������ε��ж�����AA֤����AMN�ס�ABP��
��3�����ڣ���x��0����y��kx��3��y��3����OA��BD��3��Ȼ���ɹ��ɶ������AB��5���������������ε����Ʊ���֪���������ε�����ȣ�����������������ۣ��ٵ���P��B���Ϸ�ʱ�������������ε�����ȵõ�k24k2��0�������k��һԪ���η��̣��ڵ���P��B���·�ʱ�������������ε�����ȵõ�k2��1����4k��3���������k��һԪ���η��̣�
��1����y���ֱ��l������C�����ߣ���OA��AD��BD��AD������OA��OB��
���AOB����OAD����ADB��90�������ı���OADB�Ǿ��Σ��ߡ�C�İ뾶Ϊ2����AD��OB��4��
����P��ֱ��l�ϣ�����P������Ϊ��4��p����������PҲ��ֱ��AP�ϣ���p��4k+3��
��2������DN����AD����C��ֱ�������AND��90����
�ߡ�ADN��90������DAN����ABD��90������DAN�����ADN����ABD�����ߡ�ADN����AMN��
���ABD����AMN���ߡ�MAN����BAP�����AMN�ס�ABP
��3�����ڣ����ɣ���x��0����y��kx+3�ã�y��3����OA��BD��3��AB��![]() ��
��
��S��ABD��![]() ABDN��
ABDN��![]() ADDB��DN��
ADDB��DN��![]() ��
��![]() ����AN2��AD2��DN2��
����AN2��AD2��DN2��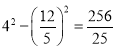 ��
��
�ߡ�AMN�ס�ABP����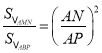 ����
����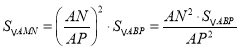
����P��B���Ϸ�ʱ����AP2��AD2+PD2��AD2+��PB��BD��2��42+��4k+3��3��2��16��k2+1����
��AP2��AD2+PD2��AD2+��BD��PB��2��42+��3��4k��3��2��16��k2+1����
S��ABP��![]() PBAD��
PBAD��![]() ��4k+3����4��2��4k+3����
��4k+3����4��2��4k+3����
��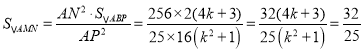 ��
��
�����ã�k2��4k��2��0�����k1��2+![]() ��k2��2��
��k2��2��![]()
����P��B���·�ʱ��
��AP2��AD2+PD2��42+��3��4k��3��2��16��k2+1����S��ABP��![]() PBAD��
PBAD��![]() [����4k+3��]��4����2��4k+3��
[����4k+3��]��4����2��4k+3��
��
����ã�k2+1������4k+3������ã�k����2��
�ۺ��������ã���k��2��![]() ��k����2ʱ����AMN���������
��k����2ʱ����AMN���������![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�