题目内容
如图所示,在同一坐标系中,作出①y=3x2②y= x2③y=x2的图象,则图象从里到外的三条抛物线对应的函数依次是(填序号) .
x2③y=x2的图象,则图象从里到外的三条抛物线对应的函数依次是(填序号) .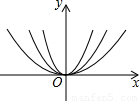
【答案】分析:抛物线的形状与|a|有关,根据|a|的大小即可确定抛物线的开口的宽窄.
解答:解:①y=3x2,
②y= x2,
x2,
③y=x2中,二次项系数a分别为3、 、1,
、1,
∵3>1> ,
,
∴抛物线②y= x2的开口最宽,抛物线①y=3x2的开口最窄.
x2的开口最宽,抛物线①y=3x2的开口最窄.
故依次填:①③②.
点评:抛物线的开口大小由|a|决定,|a|越大,抛物线的开口越窄;|a|越小,抛物线的开口越宽.
解答:解:①y=3x2,
②y=
 x2,
x2,③y=x2中,二次项系数a分别为3、
 、1,
、1,∵3>1>
 ,
,∴抛物线②y=
 x2的开口最宽,抛物线①y=3x2的开口最窄.
x2的开口最宽,抛物线①y=3x2的开口最窄.故依次填:①③②.
点评:抛物线的开口大小由|a|决定,|a|越大,抛物线的开口越窄;|a|越小,抛物线的开口越宽.

练习册系列答案
相关题目
 线l2除顶点M不动外仍经过弧A1B1(其余条件不变),那么被雨淋到的几率是扩大了还是缩小了,说明理由.
线l2除顶点M不动外仍经过弧A1B1(其余条件不变),那么被雨淋到的几率是扩大了还是缩小了,说明理由. 已知反比例函数y1=
已知反比例函数y1=