题目内容
 如图等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同速度从点D出发沿DA方向向终点A运动,其中以个动点到达端点时,另一个动点也随之停止运动
如图等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同速度从点D出发沿DA方向向终点A运动,其中以个动点到达端点时,另一个动点也随之停止运动(1)求AD的长;
(2)设CD=x,问当x为何值时△PDQ的面积达到最大?并求出最大值.
分析:(1)可通过构建直角三角形来求解:过A作AE⊥CD于E.那么可在直角三角形AED中根据两底的差和∠D的度数来求出AD的长.
2)可通过求△PDQ的面积与x的函数关系式来得出△PDQ的最大值.由于P、Q速度相同,因此CP=QD=x,那么可用x表示出PD,而△PQD中,PD边上的高=QD•sin60°,由此可根据三角形的面积公式求出S△PQD与x之间的函数关系式,可根据函数的性质求出S的最大值以及对应的x的值.
2)可通过求△PDQ的面积与x的函数关系式来得出△PDQ的最大值.由于P、Q速度相同,因此CP=QD=x,那么可用x表示出PD,而△PQD中,PD边上的高=QD•sin60°,由此可根据三角形的面积公式求出S△PQD与x之间的函数关系式,可根据函数的性质求出S的最大值以及对应的x的值.
解答:解:(1)如图1
过A作AE⊥CD,垂足为E.
依题意,DE=
=
.
在Rt△ADE中,AD=
=
×2=5;
(2)如图1
∵CP=x,h为PD边上的高,依题意,
△PDQ的面积S可表示为:
S=
PD•h=
(9-x)•x•sin60°
=
(9x-x2)
=-
(x-
)2+
.(0≤x≤5)
∴a=-
<0,
∴当x=
时(满足0≤x≤5),S最大值=
.
过A作AE⊥CD,垂足为E.

依题意,DE=
| 9-4 |
| 2 |
| 5 |
| 2 |
在Rt△ADE中,AD=
| DE |
| cos60° |
| 5 |
| 2 |
(2)如图1
∵CP=x,h为PD边上的高,依题意,
△PDQ的面积S可表示为:
S=
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 4 |
=-
| ||
| 4 |
| 9 |
| 2 |
81
| ||
| 16 |
∴a=-
| ||
| 4 |
∴当x=
| 9 |
| 2 |
81
| ||
| 16 |
点评:本题考查了学生的分析作图能力和考查学生综合运用平行线、等腰梯形、等边三角形、菱形、二次函数等知识.这里设计了一个开放的、动态的数学情境,为学生灵活运用基础知识、分析问题、解决问题留下了广阔的探索、创新的思维空间.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
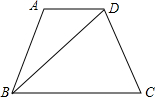 如图等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥CD.若AD=2cm,则BD=
如图等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥CD.若AD=2cm,则BD= 14、如图等腰梯形ABCD中,对角线AC,BD相交于点O,那么图中的全等三角形最多有
14、如图等腰梯形ABCD中,对角线AC,BD相交于点O,那么图中的全等三角形最多有 如图等腰梯形ABCD中,AD∥BC,∠A=110°,若将腰AB沿A→D的方向平移到DE的位置,则∠DEC=
如图等腰梯形ABCD中,AD∥BC,∠A=110°,若将腰AB沿A→D的方向平移到DE的位置,则∠DEC= 如图等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠DBC=30°,AD=5,则BC=
如图等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠DBC=30°,AD=5,则BC=