Question

从三个多项式x²+x-1，3x+2，-2x²+x-2中，任取两个多项式求和，设其和为y．
（1）求所有可能的y与x的关系式．
（2）从（1）中选出一个使y有最大值的关系式，并求出y的最大值．
（3）在平面直角坐标系中，过点P（0，m）作x轴的平行线l，当直线l与（1）中所有关系式的函数图象有6个公共点时，m的值可以为______（写出一个即可）．
（4）对于（1）中所有的关系式，在同时满足y随x的增大而增大时，直接写出x的取值范围．
[参考公式：二次函数y=ax²+bx+c图象的顶点坐标为（-，）]．

Answer 1

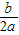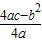【答案】分析：（1）分三种情况，分别把两个多项式相加，然后合并即可；
（2）把y=-x²+2x-3配成顶点式为y=-（x-1）²-2，利用二次函数的性质即可得到最大值；
（3）分别把三个函数配成顶点式，得到顶点坐标，然后根据它们的大致函数图象即可得到m要在-2与-3之间，在此范围取值即可；
（3）根据（3）的顶点坐标得到个抛物线的对称轴以及二次函数的性质即可得到满足条件的x的取值范围．
解答：解：（1）y=（x²+x-1）+（3x+2）=x²+4x+1；y=（x²+x-1）+（-2x²+x-2）=-x²+2x-3；y=（3x+2）+（-2x²+x-2）=-2x²+4x；

（2）y=-x²+2x-3=-（x-1）²-2，
∵a=-1＜0，
∴x=1时，y有最大值为-2；

（3）y=x²+4x+1=（x+2）²-3，顶点坐标为（-2，-3）；
y=（3x+2）+（-2x²+x-2）=-2x²+4x=-2（x-1）²+2，顶点坐标为（1，2）；
y=-x²+2x-3=-（x-1）²-2，顶点坐标为（1，-2）；
m要在-2与-3之间，可以m=-2.5；

（3）由（3）可得，同时满足y随x的增大而增大时，x的取值范围为：-2＜x＜1．
点评：本题考查了二次函数的顶点式y=a（x-k）²+h，当a＞0，x=k时，y有最小值；当a＜0，x=k时，y有最大值．