��Ŀ����
����Ŀ����֪��������A��B�����㣮
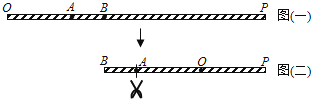
��1����ͼ1����AB=a��M��AB���е㣬CΪ�߶�AB�ϵ�һ�㣬��![]() ����AC=�� ����CB=�� ����MC=�� �����ú�a�Ĵ���ʽ��ʾ����
����AC=�� ����CB=�� ����MC=�� �����ú�a�Ĵ���ʽ��ʾ����
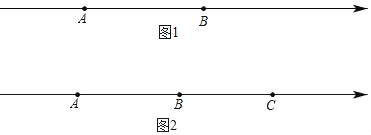
��2����ͼ2����A��B��C�����Ӧ�����ֱ�Ϊ��40����10��20��
����A��C����ͬʱ�����˶���ͬʱB�������˶�����֪��A��B��C���ٶȷֱ�Ϊ8����λ����/�롢4����λ����/�롢2����λ����/�룬��MΪ�߶�AB���е㣬��NΪ�߶�BC���е㣬��B��C����ǰ�����˶�������ʱǡ�����㣺MB=3BN��
�����ж���P��Q����C���������P��ÿ��1����λ���ȵ��ٶ����յ�A�ƶ�������P�ƶ���B��ʱ����Q�Ŵ�C�����������ÿ��3����λ���ȵ��ٶ������ƶ����ҵ���P����A��ʱ����QҲֹͣ�ƶ��������P���˶�ʱ��Ϊt������PQ�����ľ���ǡΪ18����λʱ��������������ʱ��tֵ��
���𰸡���1��![]() a��
a��![]() a��
a��![]() a����2��2��ʱǡ������MB=3BN����3����tΪ18�롢36���54��ʱ��P��Q�������18����λ���ȣ�
a����2��2��ʱǡ������MB=3BN����3����tΪ18�롢36���54��ʱ��P��Q�������18����λ���ȣ�
��������
��1�����������еĵ�����ϵ��a��ʾ��AC,CB,MC���ɣ�
��2���ټ���x��C��B�ұ�ʱ��ǡ������MB=3BN���ݴ˵ó����̣����x��ֵ���ɣ�
�ڵ�P��ʾ����Ϊ20��t����Q��ʾ����Ϊ20��3��t��30�����ٷ�������ۢٵ���P�ƶ�18��ʱ���ڵ�Q�ڵ�P���Ҳ࣬�۵���Q�ڵ�P����࣬���ɵó�����.
�⣺��1����AB=a��CΪ�߶�AB�ϵ�һ�㣬��![]() =
=![]() ��
��
��AC=![]() AB=
AB=![]() a��CB=
a��CB=![]() AB=
AB=![]() a��
a��
��M��AB���е㣬
��MC=![]() AB��
AB��![]() AB=
AB=![]() a��
a��
�ʴ�Ϊ��![]() a��
a��![]() a��
a��![]() a��
a��
��2������A��B��C�����Ӧ�����ֱ�Ϊ��40����10��20��
��AB=BC=30��
��x��ʱ��C��B�ұ�ʱ��ǡ������MB=3BN��
��BM=![]() ��8x+4x+30����BN=
��8x+4x+30����BN=![]() ��30��4x��2x����
��30��4x��2x����
����MB=3BNʱ��![]() ��8x+4x+30��=3��
��8x+4x+30��=3��![]() ��30��4x��2x����
��30��4x��2x����
��ã�x=2��
��2��ʱǡ������MB=3BN��
��3����P��ʾ����Ϊ20��t����Q��ʾ����Ϊ20��3��t��30����
������P�ƶ�18��ʱ����Qû������ʱ��PQ�����ľ���ǡΪ18����λ��
����Q�ڵ�P���Ҳ࣬��20��3��t��30������20��t��=18��
���t=36��
������Q�ڵ�P����࣬��20��t��[20��3��t��30��]=18��
���t=54��
������������tΪ18�롢36���54��ʱ��P��Q�������18����λ���ȣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�