题目内容
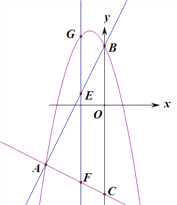
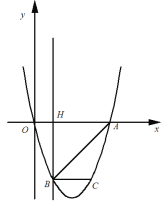
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,-3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
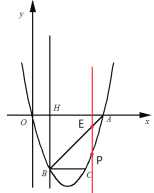
(2)点P是抛物线上一动点,当ΔABP的面积为3时,求出点P的坐标;
(3)若点M在直线BH上运动,点N在x轴上运动,点R是坐标平面内一点,当以点C、M、N、R为顶点的四边形为正方形时,请直接写出此时点R的坐标.
【答案】(1)y=x2-4x.(2)P点坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(2,-4),(3,-3).(3)R点坐标为(4,-1)、(-2,-5)、(6,2)、(0,-2).
),(2,-4),(3,-3).(3)R点坐标为(4,-1)、(-2,-5)、(6,2)、(0,-2).
【解析】
(1)把A、B两点代入解析式即可求得
(2)设直线的解析式,代入点可得到y=x-4,通过点P作y轴的平行线,则可利用已知三角形的面积求解
(3)分类讨论:①当M为直角顶点时,M在x轴下方时;②当M为直角顶点时,M在x轴上方时;③当N为直角顶点时,且N在x轴负半轴时;④当N为直角顶点时,且N在x轴正半轴时;⑤当C为直角顶点时,此种情况不存在
(1)∵抛物线y=ax2+bx过A(4,0),B(1,-3)两点,
∴![]() ,解得:
,解得:![]() ,
,
即抛物线的解析式为:y=x2-4x.
(2)设直线AB的解析式为:y=kx+c,
将A(4,0),B(1,-3)两点代入得:
∴![]() ,解得:
,解得:![]() ,
,
即直线AB的解析式为y=x-4,
过点P作PE∥y轴交直线AB于E,
则S△ABP=![]() PE×(4-1)=
PE×(4-1)=![]() PE,
PE,
∵S△ABP=3,
∴![]() PE=3,即PE=2,
PE=3,即PE=2,
设P(m,m2-4m),则H(m,m-4),
∴m2-4m-(m-4)=2或m-4-(m2-4m)=2,
解得:m= ![]() 或m=
或m= ![]() 或m=2或m=3,
或m=2或m=3,
所以P点坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(2,-4),(3,-3).
),(2,-4),(3,-3).
(3)当△CMN为等腰直角三角形时,可找到点R,使得以点C、M、N、R为顶点的四边形为正方形.
①当M为直角顶点时,M在x轴下方时,
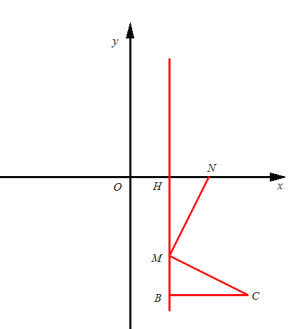
易证△MNH≌△CMB,
由C(3,-3)得:BC=HM=2,
∴BM=NH=1,即N(2,0),M(1,-2)
此时R(4,-1);
②当M为直角顶点时,M在x轴上方时,
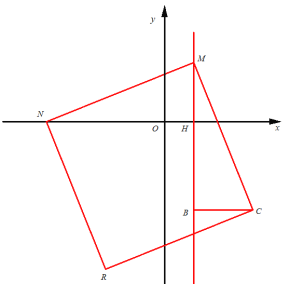
同理可得:BC=HM=2,BM=NH=5,即M(1,2),N(-4,0),C(3,-3)
此时R(-2,-5);
③当N为直角顶点时,且N在x轴负半轴时,
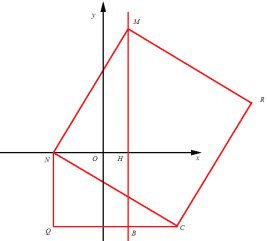
同理得:NH=NQ=3,QC=HM=5,即N(-2,0)M(1,5)C(3,-3)
此时R(6,2);
④当N为直角顶点时,且N在x轴正半轴时,
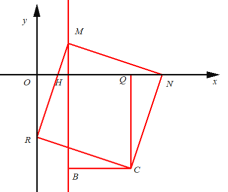
同理得:NH=CQ=3,QN=HM=1,即N(4,0)M(1,1)C(3,-3)
此时R(0,-2);
⑤当C为直角顶点时,此种情况不存在
综上所述,R点坐标为(4,-1)、(-2,-5)、(6,2)、(0,-2).

 寒假学与练系列答案
寒假学与练系列答案