题目内容
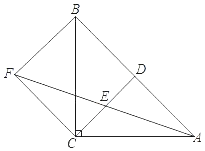
【题目】如图,以![]() 的一边AB为直径作
的一边AB为直径作![]() ,交BC于点D,交AC于点E,点D为弧BE的中点.
,交BC于点D,交AC于点E,点D为弧BE的中点.
![]() 试判断
试判断![]() 的形状,并说明理由;
的形状,并说明理由;
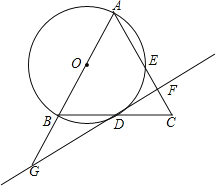
![]() 直线l切
直线l切![]() 于点D,与AC及AB的延长线分别交于点F,点G.
于点D,与AC及AB的延长线分别交于点F,点G.
![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 半径的长为m,
半径的长为m,![]() 的面积为
的面积为![]() 的面积的10倍,求BG的长
的面积的10倍,求BG的长![]() 用含m的代数式表示
用含m的代数式表示![]() .
.
【答案】(1)见解析;(2)①![]() ;②
;②![]() .
.
【解析】
![]() 连接AD,由AB为
连接AD,由AB为![]() 的直径可得出
的直径可得出![]() ,由点D为弧BE的中点利用圆周角定理可得出
,由点D为弧BE的中点利用圆周角定理可得出![]() ,利用等角的余角相等可得出
,利用等角的余角相等可得出![]() ,进而可证出
,进而可证出![]() 为等腰三角形;
为等腰三角形;
![]() 连接OD,则
连接OD,则![]() ,由
,由![]() 可得出
可得出![]() ,利用“内错角相等,两直线平行”可得出
,利用“内错角相等,两直线平行”可得出![]() ,根据平行线的性质可得出
,根据平行线的性质可得出![]() 、
、![]() ,根据等腰直角三角形的性质可得出
,根据等腰直角三角形的性质可得出![]() ,进而可得出
,进而可得出![]() ;
;
![]() 过点B作
过点B作![]() 于点H,根据等腰三角形的性质可得出
于点H,根据等腰三角形的性质可得出![]() ,利用三角形的面积结合
,利用三角形的面积结合![]() 的面积为
的面积为![]() 的面积的10倍,可得出
的面积的10倍,可得出![]() ,由
,由![]() 可得出
可得出![]() ,结合
,结合![]() 、
、![]() 可证出
可证出![]() ≌
≌![]() ,根据全等三角形的性质可得出
,根据全等三角形的性质可得出![]() ,进而可得出
,进而可得出![]() ,由
,由![]() 可得出
可得出![]() ∽
∽![]() ,根据相似三角形的性质即可求出
,根据相似三角形的性质即可求出![]()
解:![]() 是等腰三角形,理由如下:
是等腰三角形,理由如下:
连接AD,如图1所示.
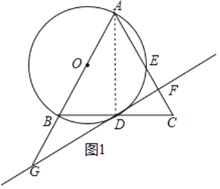
![]() 为
为![]() 的直径,
的直径,![]() .
.![]() 点D为弧BE的中点,
点D为弧BE的中点,![]() ,
,![]() ,
,![]() ,
,![]() 为等腰三角形.
为等腰三角形.![]() 连接OD,如图2所示.
连接OD,如图2所示.
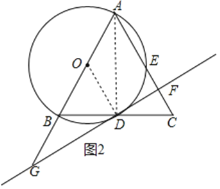
![]() 直线l是
直线l是![]() 的切线,点D是切点,
的切线,点D是切点,![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() .
.![]() 过点B作
过点B作![]() 于点H,如图3所示.
于点H,如图3所示.
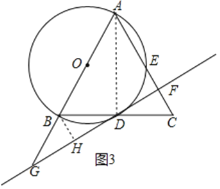
![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,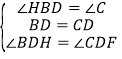 ,
,![]() ≌
≌![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() ∽
∽![]() ,
,![]() ,即
,即![]() ,
,![]()

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下两个统计图:
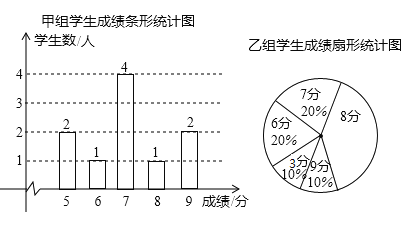
(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为 度;
(2)请补充完整下面的成绩统计分析表:
平均分 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 | 20% |
乙组 | 10% |
(3)甲组学生说他们的优秀率高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.
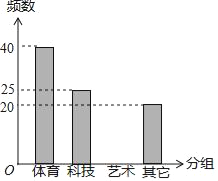
【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数 | 频率 | |
体育 | 40 | 0.4 |
科技 | 25 | a |
艺术 | b | 0.15 |
其它 | 20 | 0.2 |
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?
【题目】某区为了解全区2800名九年级学生英语口语考试成绩的情况,从中随机抽取了部分学生的成绩(满分24分,得分均为整数),制成下表:
分数段(x分) | x≤16 | 17≤x≤18 | 19≤x≤20 | 21≤x≤22 | 23≤x≤24 |
人 数 | 10 | 15 | 35 | 112 | 128 |
(1)填空:
①本次抽样调查共抽取了 名学生;
②学生成绩的中位数落在 分数段;
③若用扇形统计图表示统计结果,则分数段为x≤16的人数所对应扇形的圆心角为 °;
(2)如果将21分以上(含21分)定为优秀,请估计该区九年级考生成绩为优秀的人数.