题目内容
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 为对角线
为对角线![]() 的中点,反比例函数
的中点,反比例函数![]() 在第一象限内的图象经过点
在第一象限内的图象经过点![]() ,且与
,且与![]() 、
、![]() 分别交于
分别交于![]() 、
、![]() 两点,若四边形
两点,若四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的值为________.
的值为________.
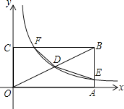
【答案】![]()
【解析】
根据反比例函数图象上的点E、F、D入手,分别找出△OCF、△OAE、矩形OABC的面积与|k|的关系,列出等式求出k值.
解:连接OF,EO,
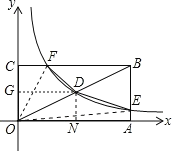
∵点D为对角线OB的中点,四边形BEDF的面积为1,
∴S△BDF=S△ODF,S△BDE=S△ODE,
∴四边形FOED的面积为1.
由题意得:E、F、D位于反比例函数图象上,则S△OCF=![]() ,S△OAE=
,S△OAE=![]() ,
,
过点D作DG⊥y轴于点G,作DN⊥x轴于点N,则S矩形ONDG=k,
∵D为矩形ABCO对角线的交点,则S矩形ABCO=4S矩形ONDG=4k,
由于函数图象在第一象限,k>0,则![]() +
+![]() +2=4k,
+2=4k,
解得:k=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目