题目内容
【题目】联想三角形内心的概念,我们可引入如下概念.
定义:到三角形的两边距离相等的点,叫做此三角形的准内心.
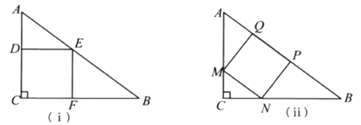
举例:如图1,若PD=PE,则点P为△ABC的准内心.
应用:如图2,BF为等边三角形的角平分线,准内心P在BF上,且PF=![]() BP,求证:点P是△ABC的内心.
BP,求证:点P是△ABC的内心.
探究:已知△ABC为直角三角形,∠C=90°,准内心P在AC上,若PC=![]() AP,求∠A的度数.
AP,求∠A的度数.

【答案】应用:见解析,探究:30°
【解析】
应用:由△ABC是等边三角形,根据等边三角形的性质得到∠ABC=60°,由角平分线的性质∴∠PBE=30°,得到PE=![]() PB,因为BF是等边△ABC的角平分线,由三线合一得到BF⊥AC,PF=
PB,因为BF是等边△ABC的角平分线,由三线合一得到BF⊥AC,PF=![]() BF,证得PE=PD=PF,得到结论P是△ABC的内心;
BF,证得PE=PD=PF,得到结论P是△ABC的内心;
探究:根据题意得:PD=PC=![]() AP,由锐角三角函数得到结论.
AP,由锐角三角函数得到结论.
应用:∵△ABC是等边三角形,
∴∠ABC=60°,
∵BF为角平分线,
∴∠PBE=30°,
∴PE=![]() PB,
PB,
∵BF是等边△ABC的角平分线,
∴BF⊥AC,
∵PF=![]() BF,
BF,
∴PE=PD=PF,
∴P是△ABC的内心;
探究:根据题意得:
PD=PC=![]() AP,
AP,
∵![]() ,
,
∴∠A是锐角,
∴∠A=30°.

练习册系列答案
相关题目