题目内容
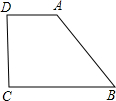如图，已知：如图梯形ABCD中，AD∥CB，AD=2，AB=5，CD=4，∠C=90°，求S梯形ABCD．
分析：求梯形面积，需求出上下底及高，在直角梯形中，运用勾股定理即可求解．
解答：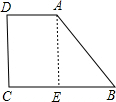
解：如图所示，过点A作AE⊥BC于E，
则四边形AECD是矩形，
∴CE=AD=2，AE=CD=4，
∴在Rt△ABE中，BE=
=3
∴BC=5，
∴S梯形ABCD=
（2+5）×4=14．
解：如图所示，过点A作AE⊥BC于E，则四边形AECD是矩形，
∴CE=AD=2，AE=CD=4，
∴在Rt△ABE中，BE=
| 52 - 42 |
∴BC=5，
∴S梯形ABCD=
| 1 |
| 2 |
点评：掌握直角梯形的性质，会求梯形的面积．
练习册系列答案
阅读快车系列答案
相关题目
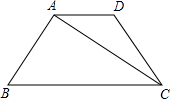已知：如图，在梯形ABCD中，AD∥BC，AB=DC，∠D=120°，对角线CA平分∠BCD，且梯形的周长为20，求AC的长及梯形面积S．
18、已知：如图梯形ABCD中，AD∥BC，AB=CD，AC与BD相交于点O．
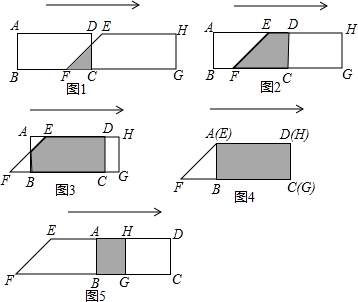
作图题：