题目内容
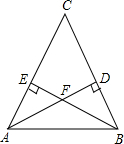已知，如图，AC=BC，BE、AD是腰上的高，求证：AD=BE．分析：由于AC=BC，那么∠EAB=∠DBA，又BE、AD是腰上的高，于是∠AEB=∠BDA=90°，再结合AB=BA，利用AAS可证△ABE≌△BAD，那么AD=BE．
解答：证明：∵AC=BC，
∴∠EAB=∠DBA，
∵BE、AD是腰上的高，
∴∠AEB=∠BDA=90°，
在△ABE和△BAD中，
∵
，
∴△ABE≌△BAD，
∴AD=BE．
∴∠EAB=∠DBA，
∵BE、AD是腰上的高，
∴∠AEB=∠BDA=90°，
在△ABE和△BAD中，
∵
|
∴△ABE≌△BAD，
∴AD=BE．
点评：本题考查了全等三角形的判定和性质，解题的关键是找出AAS需要的三个条件．
练习册系列答案
全能测控期末小状元系列答案
相关题目
29、已知：如图，AC=BD，DF=CE，∠ECB=∠FDA．求证：AF=BE．
16、已知：如图，AC=DF，AC∥FD，AE=DB，则根据
是切点，
12、已知：如图，AC、BD交于O点，OA=OC，OB=OD、则不正确的结果是（ ）
已知：如图，AC平分∠BAD，CE⊥AB于E点，CF⊥AD于F点，在AB上有一点M，且CM=CD．