题目内容
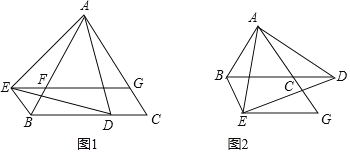
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() 是
是![]() 边上一点,作等边
边上一点,作等边![]() ,连接
,连接![]() .
.
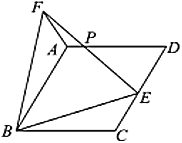
(1)求证:![]() ;
;
(2)![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)见解析;(2)12°.
【解析】
(1)根据四边形ABCD是菱形,∠ABC=60°和等边△BEF,可以证明△FAB≌△ECB,进而可得CE=AF;
(2)利用三角形的内角和定理可求∠CBE的度数.
(1)证明:∵四边形ABCD是菱形,
∴AB=BC.
∵△BEF是等边三角形,
∴BF=BE,∠FBE=∠FEB=60°.
∵∠ABC=60°,
∴∠ABC=∠FBE,
∴∠ABC-∠ABE=∠FBE-∠ABE,即∠EBC=∠FBA.
∴△EBC≌△FBC(SAS).
∴CE=AF.
(2)解:∵四边形ABCD是菱形,
∴AD∥BC,∠D=∠ABC=60°.
∴∠C=180°-∠D=120°.
在△PDE中,∠D+∠DPE+∠PED=180°,
∴∠DEP=72°.
由(1)得,∠FEB=60°,
∴∠BED=∠DEP+∠BEP=72°+60°=132°.
∴∠CBE=∠BED-∠C=132°-120°=12°.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目