题目内容
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.求证:
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)BC2=2AB•CE.

(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)BC2=2AB•CE.

证明:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
即AD是底边BC上的高,(1分)
又∵AB=AC,
∴△ABC是等腰三角形,
∴D是BC的中点;(3分)
(2)∵∠CBE与∠CAD是
所对的圆周角,
∴∠CBE=∠CAD,(5分)
又∵∠BCE=∠ACD,
∴△BEC∽△ADC;(6分)
(3)由△BEC∽△ADC,知
=
,
即CD•BC=AC•CE,(8分)
∵D是BC的中点,
∴CD=
BC,
又∵AB=AC,
∴CD•BC=AC•CE=
BC•BC=AB•CE,
即BC2=2AB•CE.(10分)
∴∠ADB=90°,
即AD是底边BC上的高,(1分)
又∵AB=AC,
∴△ABC是等腰三角形,
∴D是BC的中点;(3分)
(2)∵∠CBE与∠CAD是
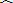 |
| DE |
∴∠CBE=∠CAD,(5分)
又∵∠BCE=∠ACD,
∴△BEC∽△ADC;(6分)
(3)由△BEC∽△ADC,知
| CD |
| CE |
| AC |
| BC |
即CD•BC=AC•CE,(8分)
∵D是BC的中点,
∴CD=
| 1 |
| 2 |
又∵AB=AC,
∴CD•BC=AC•CE=
| 1 |
| 2 |
即BC2=2AB•CE.(10分)

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目







