题目内容
如图,已知P为∠AOB的边OA上的一点,且OP=2.以P为顶点的∠MPN的两边分别交射线OB于M,N两点,且∠MPN=∠AOB=60°.当∠MPN以点P为旋转中心,PM边与PO重合的位置开始,按逆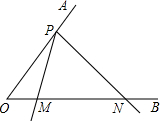 时针方向旋转(∠MPN保持不变)时,M,N两点在射线OB上同时以不同的速度向右平行移动.设OM=x,ON=y(y>x>0),△POM的面积为S.
时针方向旋转(∠MPN保持不变)时,M,N两点在射线OB上同时以不同的速度向右平行移动.设OM=x,ON=y(y>x>0),△POM的面积为S.(1)判断:△OPN与△PMN是否相似,并说明理由;
(2)写出y与x之间的关系式;
(3)试写出S随x变化的函数关系式,并确定S的取值范围.
分析:(1)已知两三角形两角对应相等,可利用AAA证相似
(2)可由(1)问的三角形相似得到y与x之间的函数关系式.
(3)根据图形得出S的关系式,然后在图形内根据x的取值范围确定S的取值范围.
(2)可由(1)问的三角形相似得到y与x之间的函数关系式.
(3)根据图形得出S的关系式,然后在图形内根据x的取值范围确定S的取值范围.
解答:解:(1)△OPN∽△PMN.
证明:在△OPN和△PMN中,
∠PON=∠MPN=60°,∠ONP=∠PNM,
∴△OPN∽△PMN;
(2)∵MN=ON-OM=y-x,
∵△OPN∽△PMN,
∴
=
,
∴PN2=ON•MN=y(y-x)=y2-xy.
过P点作PD⊥OB,垂足为D.
在Rt△OPD中,
OD=OP•cos60°=2×
=1,PD=POsin60°=
,
∴DN=ON-OD=y-1.
在Rt△PND中,
PN2=PD2+DN2=(
)2+(y-1)2=y2-2y+4,
∴y2-xy=y2-2y+4,
即y=
;
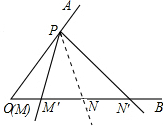
(3)在△OPM中,OM边上的高PD为
,
∴S=
•OM•PD=
•x•
=
x,
∵y>0,
∴2-x>0,即x<2.
又∵x>0,
∴x的取值范围是0<x<2.
∵S是x的正比例函数,且比例系数
>0,
∴0<S<
×2,
即0<S<
.
证明:在△OPN和△PMN中,
∠PON=∠MPN=60°,∠ONP=∠PNM,
∴△OPN∽△PMN;
(2)∵MN=ON-OM=y-x,
∵△OPN∽△PMN,
∴
| PN |
| MN |
| ON |
| PN |
∴PN2=ON•MN=y(y-x)=y2-xy.

过P点作PD⊥OB,垂足为D.
在Rt△OPD中,
OD=OP•cos60°=2×
| 1 |
| 2 |
| 3 |
∴DN=ON-OD=y-1.
在Rt△PND中,
PN2=PD2+DN2=(
| 3 |
∴y2-xy=y2-2y+4,
即y=
| 4 |
| 2-x |
(3)在△OPM中,OM边上的高PD为
| 3 |

∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∵y>0,
∴2-x>0,即x<2.
又∵x>0,
∴x的取值范围是0<x<2.
∵S是x的正比例函数,且比例系数
| ||
| 2 |
∴0<S<
| ||
| 2 |
即0<S<
| 3 |
点评:此题是一个综合性很强的题目,主要考查等边三角形的性质、三角形相似、旋转的特征、解直角三角形、函数等知识,难度很大,有利于培养同学们钻研和探索问题的精神.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 如图,已知D为BC的中点,∠BOF=∠CAE,CE⊥AD,BF⊥AD,求证:AO=2DE.
如图,已知D为BC的中点,∠BOF=∠CAE,CE⊥AD,BF⊥AD,求证:AO=2DE.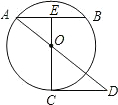 如图,已知AB为圆O的弦(非直径),E为AB的中点,EO的延长线交圆于点C,CD∥AB,且交AO的延长线于点D.EO:OC=1:2,CD=4,求圆O的半径.
如图,已知AB为圆O的弦(非直径),E为AB的中点,EO的延长线交圆于点C,CD∥AB,且交AO的延长线于点D.EO:OC=1:2,CD=4,求圆O的半径. 如图,已知P为∠AOB的平分线OP上一点,PC⊥OA于点C,∠0AP+∠0BP=180°.求证:AO+BO=2CO.
如图,已知P为∠AOB的平分线OP上一点,PC⊥OA于点C,∠0AP+∠0BP=180°.求证:AO+BO=2CO. 如图,已知P为∠AOB的平分线OP上一点,PC⊥OA于点C,∠0AP+∠0BP=180°.求证:AO+BO=2CO.
如图,已知P为∠AOB的平分线OP上一点,PC⊥OA于点C,∠0AP+∠0BP=180°.求证:AO+BO=2CO.