题目内容
【题目】如图,已知正方形ABCD的面积等于25,直线a,b,c分别过A,B,C三点,且a∥b∥c,EF⊥直线c,垂足为点F交直线a于点E,若直线a,b之间的距离为3,则EF=( )
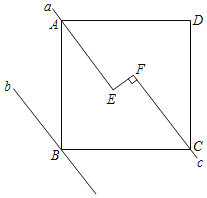
A. 1B. 2C. ![]() -3D. 5-
-3D. 5-![]()
【答案】A
【解析】
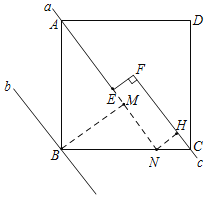
延长AE交BC于N点,过B点作BM⊥AN于M点,过N点作NH⊥FC于H点,在Rt△ABM和Rt△BMN中,易得cos∠BAM=cos∠MBN,即![]() ,解得BN=
,解得BN=![]() ,从而求出CN长度,在Rt△HNC中,利用cos∠HNC=cos∠MBN=
,从而求出CN长度,在Rt△HNC中,利用cos∠HNC=cos∠MBN=![]() ,求出NH长度,最后借助EF=NH即可.
,求出NH长度,最后借助EF=NH即可.
解:延长AE交BC于N点,过B点作BM⊥AN于M点,过N点作NH⊥FC于H点,
因为正方形的面积为25,所以正方形的边长为5.
在Rt△ABM中,AB=5,BM=3,利用勾股定理可得AM=4.
∵∠BAM+∠ABM=90°,∠NBM+∠ABM=90°,
∴∠MBN=∠BAM.
∴cos∠BAM=cos∠MBN,即![]() ,解得BN=
,解得BN=![]() .
.
∴CN=BC-BN=![]() .
.
∵∠HNC=∠MBN,
∴cos∠HNC=cos∠MBN=![]() .
.
∴![]() ,解得NH=1.
,解得NH=1.
∵a∥c,EF⊥FC,NH⊥FC,
∴EF=NH=1.
故选:A.

练习册系列答案
相关题目