Question

将背面相同，正面分别标有1，2，3，4的四张卡片洗匀后，背面朝上放在桌子上．
（1）从中随机抽取两张卡片，求卡片正面上的数字之和大于4的概率；
（2）若先从中随机抽取一张卡片（不放回），将该卡片正面上的数字作为十位上的数字；再随机抽取一张，将该卡片正面上的数字作为个位上的数字，求组成两位数恰好是3的倍数的概率（请用树状图或列表法加以说明）．

Answer 1

分析：（1）根据题意画出树状图，然后根据树状图即可求得所有等可能的结果与卡片正面上的数字之和大于4的情况，然后利用概率公式求解即可求得答案；
（2）根据（1）中的树状图即可求得所有等可能的结果与组成两位数恰好是3的倍数的情况，然后利用概率公式求解即可求得答案；

解答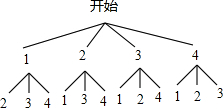：解：（1）画树状图得：
∴一共有12种等可能的结果，卡片正面上的数字之和大于4的有（1，4），（2，3），（2，4），（3，2），（3，4），（4，1），（4，2），（4，3）共8种情况，
∴卡片正面上的数字之和大于4的概率为：

8

12

=

2

3

；

（2）树状图同（1）：
∴一共有12种等可能的结果，组成两位数恰好是3的倍数的有：12，21，24，42共4种情况，
∴组成两位数恰好是3的倍数的概率为：

4

12

=

1

3

．

点评：此题考查了树状图法与列表法求概率．此题难度不大，解题的关键是根据题意画出树状图或列出表格，注意树状图法与列表法可以不重不漏的表示出所有等可能的结果，注意用到的知识点为：概率=所求情况数与总情况数之比．