题目内容
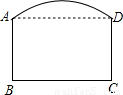
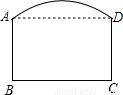
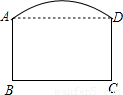
如图是一单位拟建的大门示意图,上部是一段直径为10米的圆弧形,下部是矩形ABCD,其中AB=3.7米,BC=6米,则弧AD的中点到BC的距离是 米.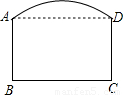
【答案】分析:先构造出半径和弦心距的直角三角形,求出弦心距,根据半径求出弧顶距弦AD的长,再加上矩形的宽.
解答: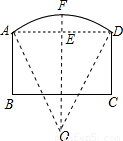 解:如图,作OE⊥AD于点E,交弧AD于F,连接OA、OD,
解:如图,作OE⊥AD于点E,交弧AD于F,连接OA、OD,
则根据垂径定理得AE= AD=
AD= BC=3米.
BC=3米.
∵直径为10米,
∴半径OA= ×10=5米,
×10=5米,
在Rt△AOE中,根据勾股定理OE=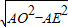 =
=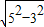 =4,
=4,
则EF=5-4=1(米),
1+3.7=4.7(米),
弧AD的中点到BC的距离是4.7米.
点评:构造半径和弦心距的直角三角利用勾股定理求弦心距是解此题突破口,也是解题的关键.
解答:
 解:如图,作OE⊥AD于点E,交弧AD于F,连接OA、OD,
解:如图,作OE⊥AD于点E,交弧AD于F,连接OA、OD,则根据垂径定理得AE=
 AD=
AD= BC=3米.
BC=3米.∵直径为10米,
∴半径OA=
 ×10=5米,
×10=5米,在Rt△AOE中,根据勾股定理OE=
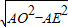 =
=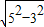 =4,
=4,则EF=5-4=1(米),
1+3.7=4.7(米),
弧AD的中点到BC的距离是4.7米.
点评:构造半径和弦心距的直角三角利用勾股定理求弦心距是解此题突破口,也是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
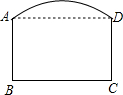 如图是一单位拟建的大门示意图,上部是一段直径为10米的圆弧形,下部是矩形ABCD,其中AB=3.7米,BC=6米,则弧AD的中点到BC的距离是
如图是一单位拟建的大门示意图,上部是一段直径为10米的圆弧形,下部是矩形ABCD,其中AB=3.7米,BC=6米,则弧AD的中点到BC的距离是