题目内容
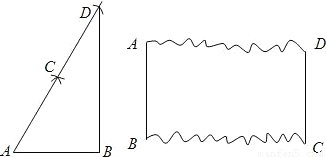
A.某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.方法是:①画线段AB,分别以A,B为圆心,AB长为半径画弧相交于C;
②以C为圆心,仍以AB长为半径画弧交AC的延长线于D;
③连接DB.则∠ABD就是直角.
(1)请你就∠ABD是直角作出合理解释;
(2)现有一长方形木块的残留部分如图,其中AB,CD整齐且平行,BC,AD是参差不齐的毛边.请你在毛边附近用尺规画一条与AB,CD都垂直的边(不写作法,保留作图痕迹);
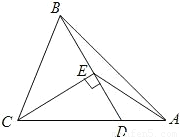
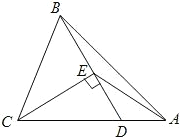
B.如图,在△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.
(1)写出图中所有相等的线段,并选择其中一对给予证明;
(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由.
【答案】分析:A(1)在连接BC后,由作图过程可知,AC=BC=AB=CD所以∠1=∠2,∠4=∠5,又∠1+∠2+∠5+∠4=2(∠2+∠5)=180°所以∠ABD=90°
(2)作图过程可以参照(1),解释相同.
B(1)因为CE和BD垂直,且∠BDC=60°,所以∠ECD=30°,所以ED= CD,又CD=2DA,所以DE=DA.∠DAE=∠DEA=30°,CE=EA
CD,又CD=2DA,所以DE=DA.∠DAE=∠DEA=30°,CE=EA
又∠DAB=45°,∴∠ABD=∠CDB-∠BAD=15°,所以BE=AE.
(2)△ADE∽△AEC,又(1)知,∠EAD=DEA=∠ACE,所以△ADE∽△AEC.
解答: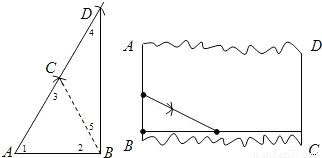 A题解:(1)解法一:由作图知,AB=BC=CD=AB,∴BC=
A题解:(1)解法一:由作图知,AB=BC=CD=AB,∴BC= AD
AD
根据三角形一边上的中线等于这边的一半,
那么这个三角形是直角三角形,
这条边所对的角就是直角,即∠ABD是直角.
解法二:由作图知,AC=BC=CD=AB,
所以△ABC为等边三角形.△BCD为等腰三角形,
∠1=∠2=∠3=60°,∠4=∠5,∠3=∠4+∠5=60°,∠5=30°,
∴∠ABD=90度.
(本题说明方法较多,只要合理均可给分)
(2)(3分)如图所示.
B题解:(1)ED=DA,EA=EB=EC.(2分)
证明:∵CE⊥BD,∴△CED是Rt△.(3分)
∵∠BDC=60°,∴∠ECD=30度.(4分)
∴CD=2DE.(5分)
∵CD=2DA,∴DE=DA.(6分)
(2)有.△ADE∽△AEC.
点评:此题考查了直角的作法,以及相似三角形的判定,难易程度适中.
(2)作图过程可以参照(1),解释相同.
B(1)因为CE和BD垂直,且∠BDC=60°,所以∠ECD=30°,所以ED=
 CD,又CD=2DA,所以DE=DA.∠DAE=∠DEA=30°,CE=EA
CD,又CD=2DA,所以DE=DA.∠DAE=∠DEA=30°,CE=EA又∠DAB=45°,∴∠ABD=∠CDB-∠BAD=15°,所以BE=AE.
(2)△ADE∽△AEC,又(1)知,∠EAD=DEA=∠ACE,所以△ADE∽△AEC.
解答:
 A题解:(1)解法一:由作图知,AB=BC=CD=AB,∴BC=
A题解:(1)解法一:由作图知,AB=BC=CD=AB,∴BC= AD
AD根据三角形一边上的中线等于这边的一半,
那么这个三角形是直角三角形,
这条边所对的角就是直角,即∠ABD是直角.
解法二:由作图知,AC=BC=CD=AB,
所以△ABC为等边三角形.△BCD为等腰三角形,
∠1=∠2=∠3=60°,∠4=∠5,∠3=∠4+∠5=60°,∠5=30°,
∴∠ABD=90度.
(本题说明方法较多,只要合理均可给分)
(2)(3分)如图所示.
B题解:(1)ED=DA,EA=EB=EC.(2分)
证明:∵CE⊥BD,∴△CED是Rt△.(3分)
∵∠BDC=60°,∴∠ECD=30度.(4分)
∴CD=2DE.(5分)
∵CD=2DA,∴DE=DA.(6分)
(2)有.△ADE∽△AEC.
点评:此题考查了直角的作法,以及相似三角形的判定,难易程度适中.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.
某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.
 某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.方法是:
某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.方法是: 某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.方法是:
某中学师生在劳动基地活动时,看到木工师傅在材料边角处画直角时,用了一种“三弧法”.方法是:
