题目内容
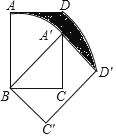
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是_____.
【答案】![]() <m≤1
<m≤1
【解析】
先将二次函数的表达式化为顶点式,确定出图象的顶点,可以直接得到(2,0)、(2,﹣1)、(2,﹣2)三点必在所要求的区域内,然后向外扩充4个整点,找到点(1,0)、 (3,0)、(1,﹣1)、(3,﹣1),然后讨论①当点(1,-1)在边界时,此时求得m=1,确定抛物线与x轴交点的横坐标,从而判断出当m=1时,恰好有7个整点符合题意,根据抛物线的开口大小与二次项系数的关系确定出0<m≤1;②当点(1,-1)在区域内时,如图2,此时若该抛物线经过点(0,0)和点(4,0),显然这两个点符合题意,将(0,0)代入y=mx2﹣4mx+4m﹣2求得m=![]() ,由此可得m=
,由此可得m=![]() 时,有9个整点符合题意,判断出m=
时,有9个整点符合题意,判断出m=![]() 不符合题意,确定出m>
不符合题意,确定出m>![]() ,综合①②的讨论即可确定出m的取值范围.
,综合①②的讨论即可确定出m的取值范围.
∵y=mx2﹣4mx+4m﹣2=m(x﹣2)2﹣2且m>0,
∴该抛物线开口向上,顶点坐标为(2,﹣2),对称轴是直线x=2,
∴点(2,0)、点(2,﹣1)、顶点(2,﹣2) 三点必在抛物线在A、B之间的部分与线段AB所围成的区域,
又∵该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,
∴必有点(1,0)、 (3,0)、(1,﹣1)、(3,﹣1),
①当点(1,-1)在边界时,
将(1,﹣1)代入y=mx2﹣4mx+4m﹣2得到﹣1=m﹣4m+4m﹣2,解得m=1,
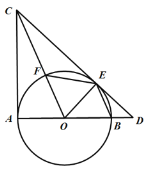
此时抛物线解析式为y=x2﹣4x+2,(如图1),
由y=0得x2﹣4x+2=0.解得x1=2﹣![]() ≈0.6,x2=2+
≈0.6,x2=2+![]() ≈3.4,
≈3.4,
∴x轴上的点(1,0)、(2,0)、(3,0)符合题意,
则当m=1时,恰好有 (1,0)、(2,0)、(3,0)、(1,﹣1)、(3,﹣1)、(2,﹣1)、(2,﹣2)这7个整点符合题意,
∴m≤1,
∴0<m≤1,【注:m的值越大,抛物线的开口越小,m的值越小,抛物线的开口越大】

②当点(1,-1)在区域内时,如图2,此时若该抛物线经过点(0,0)和点(4,0),显然这两个点符合题意,
此时x轴上的点 (1,0)、(2,0)、(3,0)也符合题意,
将(0,0)代入y=mx2﹣4mx+4m﹣2得到0=0﹣4m+0﹣2.解得m=![]() ,
,
此时抛物线解析式为y=![]() x2﹣2x,
x2﹣2x,
当x=1时,得y=![]() ×1﹣2×1=﹣
×1﹣2×1=﹣![]() <﹣1,
<﹣1,
∴点(1,﹣1)符合题意,
当x=3时,得y=![]() ×9﹣2×3=﹣
×9﹣2×3=﹣![]() <﹣1.
<﹣1.
∴点(3,﹣1)符合题意,
综上可知:当m=![]() 时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,﹣1)、(3,﹣1)、(2,﹣2)、(2,﹣1)都符合题意,共有9个整点符合题意,
时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,﹣1)、(3,﹣1)、(2,﹣2)、(2,﹣1)都符合题意,共有9个整点符合题意,
∴m=![]() 不符合题意,
不符合题意,
∴m>![]() ,
,
综合①②可得:当![]() <m≤1时,该函数的图象与x轴所围成的区域(含边界)内有七个整点,
<m≤1时,该函数的图象与x轴所围成的区域(含边界)内有七个整点,
故答案为:![]() <m≤1.
<m≤1.

【题目】小强的妈妈想在自家的院子里用竹篱笆围一个面积为4平方米的矩形小花园,妈妈问九年级的小强至少需要几米长的竹篱笆(不考虑接缝).
小强根据他学习函数的经验做了如下的探究.下面是小强的探究过程,请补充完整:
建立函数模型:
设矩形小花园的一边长为x米,篱笆长为y米.则y关于x的函数表达式为________;列表(相关数据保留一位小数):
根据函数的表达式,得到了x与y的几组值,如下表:
x | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
y | 17 | 10 | 8.3 | 8.2 | 8.7 | 9.3 | 10.8 | 11.6 |
描点、画函数图象:
如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
观察分析、得出结论:
根据以上信息可得,当x=________时,y有最小值.
由此,小强确定篱笆长至少为________米.
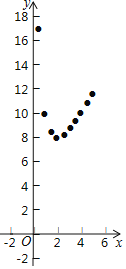
【题目】2019年4月23日是中国海军成立70周年的日子,我国在山东青岛举行了国际海上大阅兵.为增强爱国意识,某校以此次大阅兵为契机,开展了“学习海军知识,增强爱国意识”答题比赛,进入决赛的10名同学的答题情况(共7道题)如下表所示:
答对题目数量(道) | 3 | 4 | 5 | 6 | 7 |
人数(人) | 1 | 2 | 4 | 2 | 1 |
则关于答对题目数量,下列说法正确的是( )
A.平均数是2.5B.中位数是4.5C.众数是5D.方差是4