题目内容
根据下列证明过程填空：
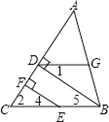
如图，BD⊥AC，EF⊥AC，D、F分别为垂足，且∠1=∠FEC，求证：∠ADG=∠C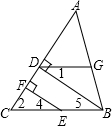
证明：∵BD⊥AC，EF⊥AC（已知）
∴∠2=∠3=90°
∴BD∥EF（同位角相等，两直线平行）
∴∠FEC=________（两直线平行，同位角相等）
∵∠1=∠FEC（已知）
∴∠1=________（等量代换）
∴DG∥BC（________）
∴∠ADG=∠C（________）
∠5 ∠5 内错角相等，两直线平行 两直线平行，同位角相等
分析：熟悉平行线的性质和判定，能正确运用语言叙述理由．
解答：证明：∵BD⊥AC，EF⊥AC（已知），
∴∠2=∠3=90°，
∴BD∥EF（同位角相等，两直线平行），
∴∠FEC=∠5（两直线平行，同位角相等）；
∵∠1=∠FEC（已知），
∴∠1=∠5（等量代换），
∴DG∥BC（内错角相等，两直线平行），
∴∠ADG=∠C（两直线平行，同位角相等）．
点评：注意平行线的性质和判定的综合运用．
分析：熟悉平行线的性质和判定，能正确运用语言叙述理由．
解答：证明：∵BD⊥AC，EF⊥AC（已知），
∴∠2=∠3=90°，
∴BD∥EF（同位角相等，两直线平行），
∴∠FEC=∠5（两直线平行，同位角相等）；
∵∠1=∠FEC（已知），
∴∠1=∠5（等量代换），
∴DG∥BC（内错角相等，两直线平行），
∴∠ADG=∠C（两直线平行，同位角相等）．
点评：注意平行线的性质和判定的综合运用．
练习册系列答案
相关题目
27、根据下列证明过程填空：
