题目内容
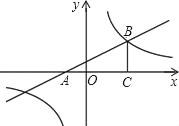
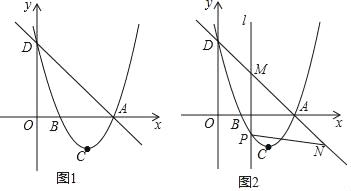
【题目】如图1,一次函数y=﹣x+3的图象交x轴于点A,交y轴于点D,抛物线y=ax2+bx+c(a≠0)的顶点为C,其图象过A、D两点,并与x轴交于另一个点B(B点在A点左侧),若![]() ;
;
(1)求此抛物线的解析式;
(2)连结AC、BD,问在x轴上是否存在一个动点Q,使A、C、Q三点构成的三角形与△ABD相似.如果存在,求出Q点坐标;如果不存在,请说明理由.
(3)如图2,若点P是抛物线上一动点,且在直线AD下方,(点P不与点A、点D重合),过点P作y轴的平行线l与直线AD交于点M,点N在直线AD上,且满足△MPN∽△ABD,求△MPN面积的最大值.
【答案】(1)y=x2﹣4x+3;(2)见解析;(3)△MPN的面积的最大值为:![]() .
.
【解析】
(1)利用一次函数解析式确定D(3,0);A(3,0),则可判断△OAD为等腰直角三角形,再计算出AB=2得到B(1,0),然后利用待定系数确定抛物线解析式;
(2)作CH⊥x轴,如图1,先利用二次函数的性质得到C(3,﹣1),再判断△ACH为等腰直角三角形得到∠CAH=45°,AC=![]() ,则∠CAQ=∠DAB,根据相似三角形的判定方法,当
,则∠CAQ=∠DAB,根据相似三角形的判定方法,当![]() 时,△AQC∽△ADB,即
时,△AQC∽△ADB,即![]() ,当
,当![]() 时,△AQC∽△ABD,即
时,△AQC∽△ABD,即![]() ,然后分别求出对应的AQ的值,从而得到对应的Q点的坐标;
,然后分别求出对应的AQ的值,从而得到对应的Q点的坐标;
(3)作PE⊥AD于E,如图2,利用相似三角形的性质得到MN=![]() MP,设P(x,x2﹣4x+3),则M(x,﹣x+3),所以MP=﹣x+3﹣(x2﹣4x+3),根据二次函数的性质,当x=
MP,设P(x,x2﹣4x+3),则M(x,﹣x+3),所以MP=﹣x+3﹣(x2﹣4x+3),根据二次函数的性质,当x=![]() 时,MP有最大值
时,MP有最大值![]() ,则MN的最大值为
,则MN的最大值为![]() ,接着确定PE的最大值为
,接着确定PE的最大值为![]() ,然后根据三角形面积公式计算出△MPN的面积的最大值.
,然后根据三角形面积公式计算出△MPN的面积的最大值.
解:(1)当x=0时,y=﹣x+3=3,则D(3,0);
当y=0时,﹣x+3=0,解得x=3,则A(3,0),
∵OD=OA,
∴△OAD为等腰直角三角形,
∴AD=3![]() ,
,
∵![]() ,
,
∴AB=2,
∴B(1,0),
设抛物线解析式为y=a(x﹣1)(x﹣3),
把D(0,3)代入得a(﹣1)(﹣3)=3,解得a=1,
∴抛物线解析式为y=(x﹣1)(x﹣3),即y=x2﹣4x+3;
(2)作CH⊥x轴,如图1,
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴C(2,﹣1)
∴AH=CH=1,
∴△ACH为等腰直角三角形,
∴∠CAH=45°,AC=![]() ,
,
∵△OAD为等腰直角三角形,
∴∠DAO=45°,
∵∠CAQ=∠DAB,
∴当![]() 时,△AQC∽△ADB,即
时,△AQC∽△ADB,即![]() ,解得AQ=3,此时Q(0,0);
,解得AQ=3,此时Q(0,0);
当![]() 时,△AQC∽△ABD,即
时,△AQC∽△ABD,即![]() ,解得AQ=
,解得AQ=![]() ,此时Q(
,此时Q(![]() ,0);
,0);
综上所述,Q点的坐标为(0,0)或(![]() ,0);
,0);
(3)作PE⊥AD于E,如图2,
∵△MPN∽△ABD,
∴![]() ,
,
∴MN=![]() MP,
MP,
设P(x,x2﹣4x+3),则M(x,﹣x+3),
∴MP=﹣x+3﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣![]() )2+
)2+![]() ,
,
当x=![]() 时,MP有最大值
时,MP有最大值![]() ,
,
∴MN的最大值为![]() =
=![]() ,
,
∵∠PME=45°,
∴PE=![]() PM,
PM,
∴PE的最大值为![]() ×
×![]() =
=![]() ,
,
∴△MPN的面积的最大值为![]() ×
×![]() ×
×![]() =
=![]() .
.

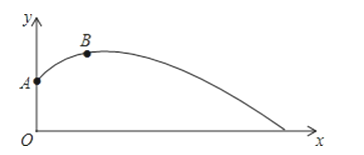
【题目】小明为了检测自己实心球的训练情况,再一次投掷的测试中,实心球经过的抛物线如图所示,其中出手点A的坐标为(0,![]() ),球在最高点B的坐标为(3,
),球在最高点B的坐标为(3,![]() ).
).
(1)求抛物线的解析式;
(2)已知某市男子实心球的得分标准如表:
得分 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
掷远(米) | 8.6 | 8.3 | 8 | 7.7 | 7.3 | 6.9 | 6.5 | 6.1 | 5.8 | 5.5 | 5.2 | 4.8 | 4.4 | 4.0 | 3.5 | 3.0 |
假设小明是春谷中学九年级的男生,求小明在实心球训练中的得分;
(3)在小明练习实心球的正前方距离投掷点7米处有一个身高1.2米的小朋友在玩耍,问该小朋友是否有危险(如果实心球在小孩头顶上方飞出为安全,否则视为危险),请说明理由.