题目内容
如果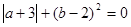 ,则
,则 .
.
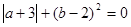 ,则
,则 .
.1
首先根据非负数的性质可求出a、b的值,进而可求出(a+b)2010的值.
解:∵|a+3|+(b-2)2=0,
∴a+3=0,b-2=0,
∴a=-3,b=2;
因此(a+b)2010=(-3+2)2010=1.
故答案为:1.
解:∵|a+3|+(b-2)2=0,
∴a+3=0,b-2=0,
∴a=-3,b=2;
因此(a+b)2010=(-3+2)2010=1.
故答案为:1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
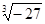 =3
=3 与比
与比 小10的数的积”是( )
小10的数的积”是( ) ;
;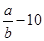 ;
; ;
; 。
。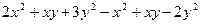 ,并求当x=2,y=1时,代数式的值.
,并求当x=2,y=1时,代数式的值.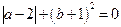 ,求
,求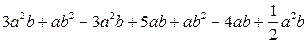 的值.
的值.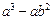 .
.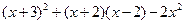 ,其中
,其中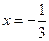 .
.