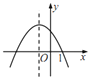题目内容
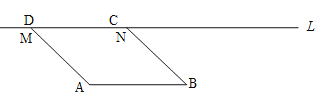
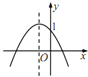
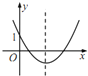
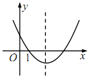
【题目】如图,在正方形网格中,∠1、∠2、∠3的大小关系( )
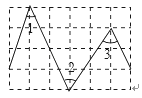
A.∠1=∠2=∠3B.∠1<∠2<∠3C.∠1=∠2>∠3D.∠1<∠2=∠3
【答案】D
【解析】
由平行线的性质可知:∠CBD=∠BDE,∠EDF=∠DFG,然后根据锐角三角形函数的定义可知:tan∠ABC=![]() ,tan∠EDF=
,tan∠EDF=![]() ,tan∠BDE=tan∠GFH=
,tan∠BDE=tan∠GFH=![]() ,从而可判定出∠ABC<∠EDF,∠BDE=∠GFH.然后即可比较它们的大小.
,从而可判定出∠ABC<∠EDF,∠BDE=∠GFH.然后即可比较它们的大小.
如图所示:

根据图形可知:
∠CBD=∠BDE,tan∠ABC=![]() ,tan∠EDF=
,tan∠EDF=![]() ,
,
∴∠ABC<∠EDF
∴∠ABC+∠CBD<∠EDF+∠BDE,即∠1<∠2.
根据图形可知:∠EDF=∠DFG,tan∠BDE=![]() ,tan∠GFH=
,tan∠GFH=![]() ,
,
∴∠BDE=∠GFH.
∴∠EDF+∠BDE=∠DFG+∠GFH,即:∠2=∠3.
故选D.

练习册系列答案
相关题目