题目内容
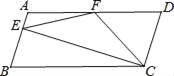
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 以每秒1个单位长度的速度从点
以每秒1个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动;点
运动;点![]() 同时以每秒3个单位长度的速度从点
同时以每秒3个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动,点
运动,点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.
也随之停止运动.
(1)当运动时间![]() 为多少秒时,
为多少秒时,![]() ;
;
(2)当运动时间![]() 为多少秒时,以点
为多少秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
(3)![]() ,
,![]() ,求
,求![]() 的面积关于运动时间
的面积关于运动时间![]() 的函数关系和自变量
的函数关系和自变量![]() 的取值范围.
的取值范围.
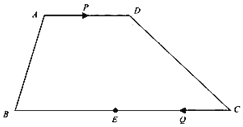
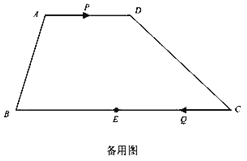
【答案】(1)当运动时间![]() 为1.5秒时,
为1.5秒时,![]() ;(2)当运动时间
;(2)当运动时间![]() 为1秒或3.5秒时,以点
为1秒或3.5秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形;(3)
为顶点的四边形是平行四边形;(3)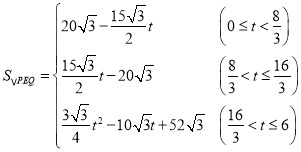
【解析】
(1)根据![]() 、
、![]() 可判定四边形
可判定四边形![]() 为平行四边形,此时
为平行四边形,此时![]() ,可得方程
,可得方程![]() ,解方程即可得解;
,解方程即可得解;
(2)分别从当![]() 在
在![]() 上时,四边形
上时,四边形![]() 为平行四边形和当
为平行四边形和当![]() 在
在![]() 上时,四边形
上时,四边形![]() 为平行四边形两方面分析求解即可求得答案;
为平行四边形两方面分析求解即可求得答案;
(3)分别从当![]() 在线段
在线段![]() 上时、当
上时、当![]() 与
与![]() 重合时、当
重合时、当![]() 在线段
在线段![]() 上时、当
上时、当![]() 在线段
在线段![]() 上时四方面进行讨论,从而确定
上时四方面进行讨论,从而确定![]() 的面积关于运动时间
的面积关于运动时间![]() 的函数关系和自变量
的函数关系和自变量![]() 的取值范围.
的取值范围.
解:(1)如图示,
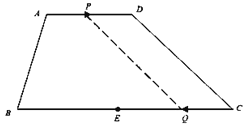
∵![]() ,
,![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]()
又∵![]() ,
,![]()
∴![]() .
.
当运动时间![]() 为1.5秒时,
为1.5秒时,![]() .
.
(2)由题意知,此时有两种情况,![]() 在
在![]() 上或
上或![]() 在
在![]() 上,
上,
①当![]() 在
在![]() 上时,四边形
上时,四边形![]() 为平行四边形
为平行四边形
此时![]() ,
,
又∵![]() ,
,![]()
∴![]()
∴![]()
∴![]() 满足题意
满足题意
②当![]() 在
在![]() 上时,四边形
上时,四边形![]() 为平行四边形
为平行四边形
此时![]() .
.
又∵![]() ,
,![]()
∴![]()
∴![]()
∴![]() 满足题意;
满足题意;
当运动时间![]() 为1秒或3.5秒时,以点
为1秒或3.5秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
(3)如图,过点![]() 作,
作,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
∵![]() ,
,![]()
∴![]()
∴![]() .
.
∴![]()
①如图(1),
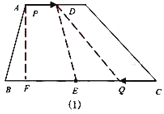
当![]() 在线段
在线段![]() 上时,
上时,![]() .
.
此时![]() ,
,![]() ,即:
,即:![]()
![]()
![]() .
.
②当![]() 与
与![]() 重合时,
重合时,![]() ,此时
,此时![]() 不存在;
不存在;
③当![]() 在线段
在线段![]() 上时,如图(2)
上时,如图(2)

![]()
此时![]() ,且
,且![]()
即:![]()
![]()
![]()
④当![]() 在线段
在线段![]() 上时,如图(3),联结
上时,如图(3),联结![]() ,过
,过![]() 作
作![]() ,交
,交![]() 于点
于点![]()
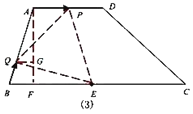
此时![]() ,且
,且![]() ,即:
,即:![]() .
.
![]() 梯形
梯形![]()
![]()
又∵![]()
∴![]()
∴![]()
∴![]() .
.
∴![]()
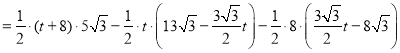
![]()
综上所述,![]() 的面积关于运动时间
的面积关于运动时间![]() 的函数关系及自变量
的函数关系及自变量![]() 的取值范围为
的取值范围为
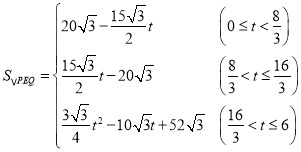
故答案是:(1)当运动时间![]() 为1.5秒时,
为1.5秒时,![]() ;(2)当运动时间
;(2)当运动时间![]() 为1秒或3.5秒时,以点
为1秒或3.5秒时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形;(3)
为顶点的四边形是平行四边形;(3)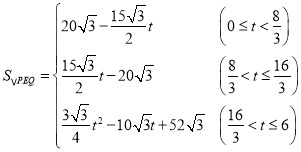 .
.